题目内容
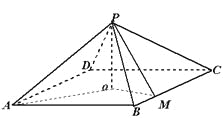
【题目】如图,四棱锥![]() 中,底面是以
中,底面是以![]() 为中心的菱形,
为中心的菱形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() 为
为![]() 上一点,且
上一点,且![]() .
.
(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)因为![]() 底面
底面![]() ,所以有
,所以有![]() ,因此欲证
,因此欲证![]() 平面
平面![]() ,只要证
,只要证![]() ,而这一点可通过连结
,而这一点可通过连结![]() ,利用菱形的性质及勾股定理解决.
,利用菱形的性质及勾股定理解决.
(2)欲求四棱锥![]() 的体积.,必须先求出
的体积.,必须先求出![]() ,连结
,连结![]() ,设
,设![]() ,在
,在![]() 利用余弦定理求出
利用余弦定理求出![]() ,由三个直角三角形
,由三个直角三角形![]() ,依据勾股定理建立关于
,依据勾股定理建立关于![]() 的方程即可.
的方程即可.
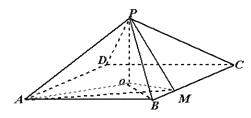
解:(1)如图,因![]() 为菱形,
为菱形, ![]() 为菱形中心,连结
为菱形中心,连结![]() ,则
,则![]() ,因
,因![]() ,故
,故![]()
又因为![]() ,且
,且![]() ,在
,在![]() 中
中
![]()
![]()
所以![]() ,故
,故![]()
又![]() 底面
底面![]() ,所以
,所以![]() ,从而
,从而![]() 与平面
与平面![]() 内两条相交直线
内两条相交直线![]() 都垂直,所以
都垂直,所以![]() 平面
平面![]()
(2)解:由(1)可知, ![]()
设![]() ,由
,由![]() 底面
底面![]() 知,
知, ![]() 为直角三角形,故
为直角三角形,故
![]()
由![]() 也是直角三角形,故
也是直角三角形,故![]()
连结![]() ,在
,在![]() 中,
中, ![]()
![]()
由已知![]() ,故
,故![]() 为直角三角形,则
为直角三角形,则
![]()
即![]() ,得
,得![]() ,
, ![]() (舍去),即
(舍去),即![]()
此时![]()
![]()
所以四棱锥![]() 的体积
的体积
![]()

练习册系列答案
相关题目