题目内容
定义在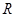 上的函数
上的函数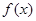 满足:
满足: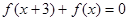 ,且函数
,且函数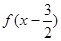 为奇函数。给出以下3个命题:
为奇函数。给出以下3个命题:
①函数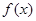 的周期是6;
的周期是6;
②函数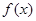 的图像关于点
的图像关于点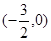 对称;
对称;
③函数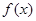 的图像关于
的图像关于 轴对称。
轴对称。
其中,真命题的个数是( )
A.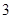 | B.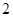 | C. | D. |
A
解析试题分析: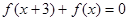
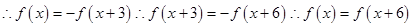
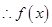 周期为6,函数
周期为6,函数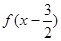 为奇函数,图像关于原点对称,向左平移
为奇函数,图像关于原点对称,向左平移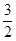 个单位得
个单位得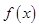 ,所以
,所以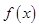 关于点
关于点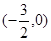 对称,
对称,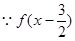 是奇函数
是奇函数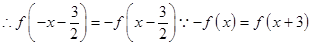
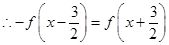
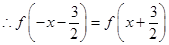 即
即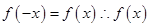 是偶函数
是偶函数
考点:函数周期性奇偶性
点评:函数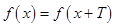 则周期为
则周期为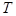 ,
,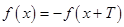 则周期为
则周期为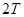 ,函数是奇函数则满足
,函数是奇函数则满足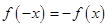 ,函数是偶函数则满足
,函数是偶函数则满足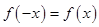

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
定义在R上的偶函数 ,对任意x1,x2∈[0,+∞),(x1≠x2),有
,对任意x1,x2∈[0,+∞),(x1≠x2),有 ,
,
则 ( )
A. | B. |
C. | D. |
若f(x)为R上的奇函数,给出下列四个说法:
①f(x)+f(-x)=0 ; ②f(x)-f(-x)=2f(x);
③f(x)·f(-x)<0; ④ 。其中一定正确的有( )
。其中一定正确的有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
已知函数 ,其导函数
,其导函数 的图象如图所示,则
的图象如图所示,则 ( )
( )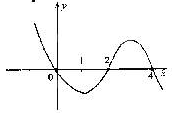
| A.在(-∞,0)上为减函数 | B.在 0处取极小值 0处取极小值 |
| C.在(4,+∞)上为减函数 | D.在 2处取极大值 2处取极大值 |
函数f(x)=log2(3x+1)的值域为( )
| A.(0,+∞) | B.[0,+∞) | C.(1,+∞) | D.[1,+∞) |
已知函数 ,若
,若 互不相等,且
互不相等,且 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
函数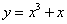 的递增区间是( )
的递增区间是( )
A.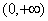 | B. | C.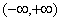 | D.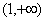 |
若函数f(x)=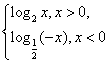 ,若f(a)>f(-a),则实数a的取值范围是( )
,若f(a)>f(-a),则实数a的取值范围是( )
| A.(-1,0)∪(0,1) | B.(-∞,-1)∪(1,+∞) |
| C.(-1,0)∪(1,+∞) | D.(-∞,-1)∪(0,1) |
已知函数f(x)=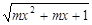 的定义域是一切实数,则m的取值范围是( )
的定义域是一切实数,则m的取值范围是( )
| A.0<m≤4 | B.0≤m≤1 | C.m≥4 | D.0≤m≤4 |