Question

【题目】如图，在三棱柱中，、分别是、的中点.

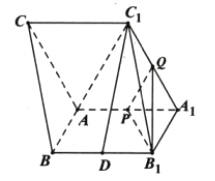
（1）设棱的中点为，证明：平面；

（2）若，，，且平面平面，求三棱柱的高.

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

（1）连接，证明出平面平面，然后利用平面与平面平行的性质可得出平面；

（2）将三棱柱的高转化成三棱锥的高来计算，过点作交于点，可得出平面，计算出的长度，然后利用等体积法由计算出三棱锥的高.

（1）连接，在三棱柱中，，

是的中点，是的中点，，四边形是平行四边形，

，平面，平面，平面.

、分别是、的中点，，

又平面，平面，平面，

，、平面，平面平面.

平面，平面；

（2）三棱柱的高转化成三棱锥的高，设为，

过点作交于点，

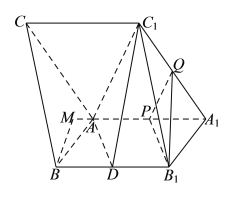
因为平面平面，平面平面，

又因为，平面，所以平面，

在中，，.

又因为，.

所以，所以，解得.

因此，三棱柱的高为.