题目内容
(本题满分14分)
已知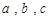 分别是
分别是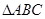 的三个内角
的三个内角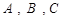 的对边,
的对边,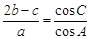 .
.
(Ⅰ)求角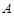 的大小;
的大小;
(Ⅱ)求函数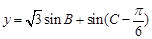 的值域.
的值域.
已知
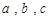 分别是
分别是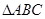 的三个内角
的三个内角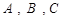 的对边,
的对边,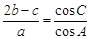 .
.(Ⅰ)求角
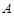 的大小;
的大小;(Ⅱ)求函数
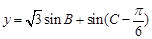 的值域.
的值域.(1) 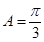 (2)
(2)
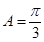 (2)
(2)
试题分析:解:(I)由正弦定理,得:
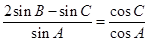 …………………………2分
…………………………2分即
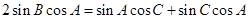
故
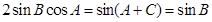 …………………………………4分
…………………………………4分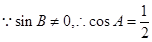
所以
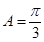 ……………………………………………………6分
……………………………………………………6分(II)
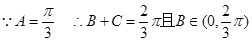 ……………………8分
……………………8分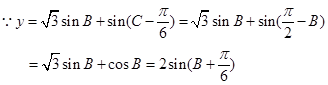 ……………………11分
……………………11分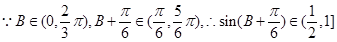 ………………13分
………………13分所以所求函数值域为
 ……………………14分
……………………14分点评:解决这类三角形和三角函数相互结合的题目,一般要对于表达式先进行化简,分析得到角或者边的大小,然后利用三角函数的性质来分析得到相应的值域。对于值域问题的考查是高考中的重点,也是热点,要熟练的掌握。

练习册系列答案
相关题目
 中,a,b,c分别是角A,B,C的对边,已知
中,a,b,c分别是角A,B,C的对边,已知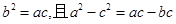
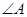 的大小;
的大小;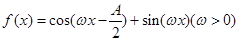 且
且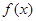 的最小正周期为
的最小正周期为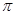 ,求
,求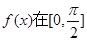 的最大值。
的最大值。 中,若
中,若 ,则
,则 的面积S= .
的面积S= . ,
,
 ,且
,且 ∥
∥ ,
, ,且△ABC的面积小于
,且△ABC的面积小于 ,求角B的取值范围.
,求角B的取值范围.
 ,则外接圆的半径为___
,则外接圆的半径为___ ,则A= ( )
,则A= ( )



 .
. ,求a,b;
,求a,b; 中,
中, 分别是角
分别是角 的对边,且
的对边,且 ,若
,若 =
= ,
, ,则△
,则△


