题目内容
(2013•青浦区一模)已
=(2cosx+2
sinx,1),
=(cosx,-y),满足
•
=0.
(1)将y表示为x的函数f(x),并求f(x)的最小正周期;
(2)已知a,b,c分别为△ABC的三个内角A,B,C对应的边长,若f(x)≤f(
)对所有的x∈R恒成立,且a=2,求b+c的取值范围.
| m |
| 3 |
| n |
| m |
| n |
(1)将y表示为x的函数f(x),并求f(x)的最小正周期;
(2)已知a,b,c分别为△ABC的三个内角A,B,C对应的边长,若f(x)≤f(
| A |
| 2 |
分析:(1)根据向量的数量积公式可求出f(x)的解析式,然后利用二倍角公式和辅助角公式进行化简,最后利用周期公式可求出所求;
(2)根据f(x)≤f(
)对所有的x∈R恒成立可求出角A,然后利用余弦定理求出b与c的等量关系,利用基本不等式和构成三角形的条件可求出b+c的取值范围.
(2)根据f(x)≤f(
| A |
| 2 |
解答:解:(1)∵
•
=0,
=(2cosx+2
sinx,1),
=(cosx,-y),
∴(2cosx+2
sinx)cosx-y=0
即f(x)=(2cosx+2
sinx)cosx
=2cos2x+2
sinxcosx
=1+cos2x+
sin2x
=1+2sin(2x+
)
T=
=π
∴f(x)的最小正周期为π.
(2)∵f(x)≤f(
)对所有的x∈R恒成立
∴1+2sin(2x+
)≤1+2sin(A+
)对所有的x∈R恒成立
即sin(2x+
)≤sin(A+
)对所有的x∈R恒成立,而A是三角形中的角
∴A=
∴cosA=cos
=
即b2+c2=4+bc即(b+c)2=4+3bc≤4+3(
)2
∴(b+c)2≤16即b+c≤4
而b+c>a=2
∴2<b+c≤4即b+c的取值范围为(2,4]
| m |
| n |
| m |
| 3 |
| n |
∴(2cosx+2
| 3 |
即f(x)=(2cosx+2
| 3 |
=2cos2x+2
| 3 |
=1+cos2x+
| 3 |
=1+2sin(2x+
| π |
| 6 |
T=
| 2π |
| 2 |
∴f(x)的最小正周期为π.
(2)∵f(x)≤f(
| A |
| 2 |
∴1+2sin(2x+
| π |
| 6 |
| π |
| 6 |
即sin(2x+
| π |
| 6 |
| π |
| 6 |
∴A=
| π |
| 3 |
∴cosA=cos
| π |
| 3 |
| b2+c2-4 |
| 2bc |
| b+c |
| 2 |
∴(b+c)2≤16即b+c≤4
而b+c>a=2
∴2<b+c≤4即b+c的取值范围为(2,4]
点评:本题主要考查了平面向量数量积的运算,以及三角函数中的恒等变换应用,同时考查了运算求解的能力,属于中档题.

练习册系列答案
相关题目
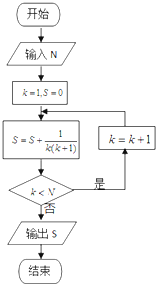 (2013•青浦区一模)如果执行如图的框图,输入N=5,则输出的数等于
(2013•青浦区一模)如果执行如图的框图,输入N=5,则输出的数等于