题目内容
已知实数x,y满足
,若(3,
)是使得ax-y取得最小值的可行解,则实数a的取值范围为
|
| 5 |
| 2 |
a≤-
| 1 |
| 2 |
a≤-
.| 1 |
| 2 |
分析:作出不等式组表示的平面区域,令z=ax-y,则y=ax-z则-z表示直线y=ax-z在y轴上的截距,截距越大,z越小,结合图象可求a的范围
解答:解:作出不等式组表示的平面区域,如图所示
令z=ax-y,则y=ax-z则-z表示直线y=ax-z在y轴上的截距,截距越大,z越小
做直线L:ax-y=0,要使得直线向上平移到A(3,
)时,z最小即综截距最大
结合图象可知,a≤-
故答案为:a≤-
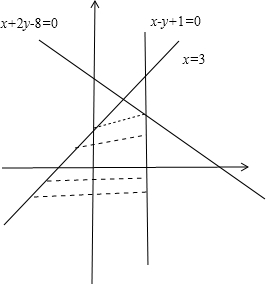
令z=ax-y,则y=ax-z则-z表示直线y=ax-z在y轴上的截距,截距越大,z越小
做直线L:ax-y=0,要使得直线向上平移到A(3,
| 5 |
| 2 |
结合图象可知,a≤-
| 1 |
| 2 |
故答案为:a≤-
| 1 |
| 2 |

点评:本题主要考查了线性规划的简单应用,当满足取得最值的最优解的个数唯一时,一般需要确定目标函数中的 直线斜率与边界斜率的比较

练习册系列答案
相关题目
已知实数x,y满足
-
=1(a>0,b>0),则下列不等式中恒成立的是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、|y|<
| ||
B、y>-
| ||
C、|y|>-
| ||
D、y<
|