题目内容
已知倾斜角为1200的直线 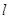 过圆C:
过圆C: 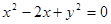 的圆心,则此直线
的圆心,则此直线 的方程是( )
的方程是( )
 过圆C:
过圆C: 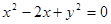 的圆心,则此直线
的圆心,则此直线 的方程是( )
的方程是( )A.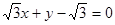 | B.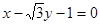 |
C.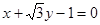 | D.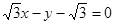 |
A
分析:把圆的方程化为标准形式,求出圆心坐标,求出直线的斜率,用点斜式求直线方程.
解答:解:圆C:x2-2x+y2="0" 即 (x-1)2+y2=1,表示圆心C(1,0),半径等于1的圆.
直线的斜率为 k=tan1200°=-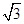 ,用点斜式求得直线l的方程是 y-0=-
,用点斜式求得直线l的方程是 y-0=-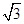 (x-1),即
(x-1),即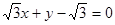
故选A.
点评:本题考查用点斜式求直线方程的方法,圆的标准方程,求出圆心坐标和直线的斜率,是解题的关键.
解答:解:圆C:x2-2x+y2="0" 即 (x-1)2+y2=1,表示圆心C(1,0),半径等于1的圆.
直线的斜率为 k=tan1200°=-
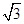 ,用点斜式求得直线l的方程是 y-0=-
,用点斜式求得直线l的方程是 y-0=-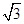 (x-1),即
(x-1),即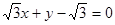
故选A.
点评:本题考查用点斜式求直线方程的方法,圆的标准方程,求出圆心坐标和直线的斜率,是解题的关键.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
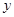 轴相切,圆心在直线
轴相切,圆心在直线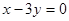 上,在
上,在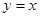 上截得的弦长为
上截得的弦长为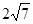 ,
,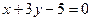 相切于点
相切于点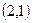 .
. 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.  +2x-4y=0的圆心,则a的值为
+2x-4y=0的圆心,则a的值为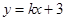 与圆
与圆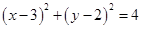 相交于M,N两点,若
相交于M,N两点,若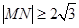 ,则
,则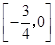
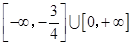
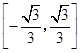
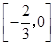
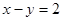 被圆
被圆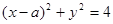 截得弦长为
截得弦长为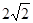 ,则实数
,则实数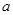 的值为( )
的值为( )
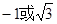
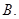
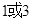
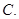
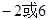
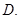

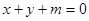 与圆
与圆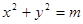 相切,则
相切,则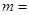 ( )
( )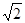
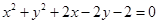 的圆心到直线3x+4y+14=0的距离是 .
的圆心到直线3x+4y+14=0的距离是 . 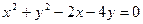 的圆心到直线
的圆心到直线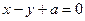 的距离为
的距离为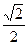 ,则a的值
,则a的值