题目内容
直线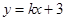 与圆
与圆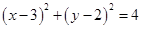 相交于M,N两点,若
相交于M,N两点,若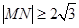 ,则
,则
k的取值范围是( )
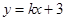 与圆
与圆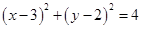 相交于M,N两点,若
相交于M,N两点,若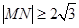 ,则
,则k的取值范围是( )
A.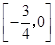 | B.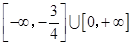 |
C.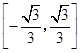 | D.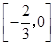 |
A
分析:先求圆心坐标和半径,求出最大弦心距,利用圆心到直线的距离不大于最大弦心距,求出k的范围.
解答:解:解法1:圆心的坐标为(3.,2),且圆与x轴相切.
当|MN|=2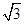 时,弦心距最大,
时,弦心距最大,
由点到直线距离公式得 ≤1
≤1
解得k∈[-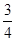 ,0];
,0];
故选A.
解法2:数形结合,
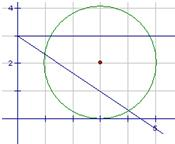
如图由垂径定理得夹在两直线之间即可,不取+∞,排除B,考虑区间不对称,排除C,利用斜率估值,
故选A.
解答:解:解法1:圆心的坐标为(3.,2),且圆与x轴相切.
当|MN|=2
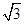 时,弦心距最大,
时,弦心距最大,由点到直线距离公式得
 ≤1
≤1解得k∈[-
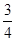 ,0];
,0];故选A.
解法2:数形结合,

如图由垂径定理得夹在两直线之间即可,不取+∞,排除B,考虑区间不对称,排除C,利用斜率估值,
故选A.

练习册系列答案
相关题目
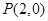 及圆
及圆 :
: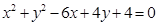 .
.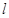 过点
过点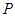 且与圆心
且与圆心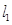 与圆
与圆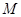 、
、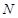 两点,当
两点,当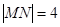 时,求以线段
时,求以线段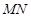 为直径的圆
为直径的圆 的方程;
的方程;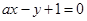 与圆
与圆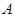 ,
,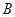 两点,是否存在实数
两点,是否存在实数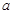 ,使得过点
,使得过点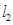 垂直平分弦
垂直平分弦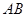 ?若存在,求出实数
?若存在,求出实数 ,直线
,直线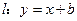 .
.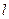 与圆C相切,求实数b的值;
与圆C相切,求实数b的值;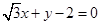 截圆
截圆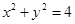 得到的弦长为
得到的弦长为

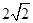
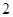
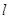 过圆C:
过圆C: 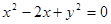 的圆心,则此直线
的圆心,则此直线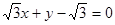
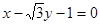
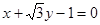
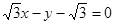
 轨迹方程
轨迹方程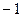 , 0),B(0, 2)的直线
, 0),B(0, 2)的直线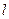 与圆
与圆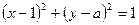 相切,求
相切,求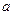 的值
的值
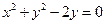 上任一点
上任一点
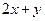 的取值范围
的取值范围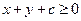 恒成立,求实数C的最小值,
恒成立,求实数C的最小值,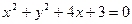 的所有切线中,求在坐标轴上截距相等的切线方程。
的所有切线中,求在坐标轴上截距相等的切线方程。