题目内容
已知函数f(x)是定义在正实数集上的单调函数,且满足对任意x>0,都有f(f(x)-lnx)=1+e,则f(1)=________.
e
f(x)-lnx必为常数函数,否则存在两个不同数,其对应值均为1+e,与单调函数矛盾.所以可设f(x)-lnx=c,则f(x)=lnx+c.将c代入,得f(c)=1+e,即lnc+c=1+e.
∵y=lnx+x是单调增函数,当c=e时,lnc+c=1+e成立,
∴f(x)=lnx+e.则f(1)=e
∵y=lnx+x是单调增函数,当c=e时,lnc+c=1+e成立,
∴f(x)=lnx+e.则f(1)=e

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 ,若函数
,若函数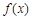 的图象恒在
的图象恒在 轴上方,求实数
轴上方,求实数 的取值范围.
的取值范围.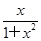 在区间[1,+∞)上是减函数.
在区间[1,+∞)上是减函数.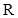 上的函数
上的函数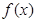 ,对任意两个不相等的实数
,对任意两个不相等的实数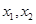 ,都有
,都有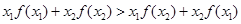 ,则称函数
,则称函数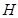 函数”.给出下列函数①
函数”.给出下列函数① ;②
;②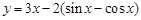 ;③
;③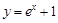 ;④
;④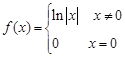 .
.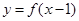 是定义在
是定义在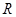 上的奇函数,则不等式
上的奇函数,则不等式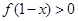 的解集为( )
的解集为( )