题目内容
(2012•洛阳模拟)已知三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2
,AB=1,AC=2,∠BAC=60°,则球O的表面积为
( )
| 3 |
( )
分析:由三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2
,AB=1,AC=2,∠BAC=60°,知BC=
,∠ABC=90°.故△ABC截球O所得的圆O′的半径r=
AC=1,由此能求出球O的半径,从而能求出球O的表面积.
| 3 |
| 3 |
| 1 |
| 2 |
解答: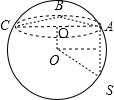 解:如图,三棱锥S-ABC的所有顶点都在球O的球面上,
解:如图,三棱锥S-ABC的所有顶点都在球O的球面上,
∵SA⊥平面ABC,SA=2
,AB=1,AC=2,∠BAC=60°,
∴BC=
=
,
∴∠ABC=90°.
∴△ABC截球O所得的圆O′的半径r=
AC=1,
∴球O的半径R=
=2,
∴球O的表面积S=4πR2=16π.
故选C.
.
 解:如图,三棱锥S-ABC的所有顶点都在球O的球面上,
解:如图,三棱锥S-ABC的所有顶点都在球O的球面上,∵SA⊥平面ABC,SA=2
| 3 |
∴BC=
| 1+4-2×1×2×cos60° |
| 3 |
∴∠ABC=90°.
∴△ABC截球O所得的圆O′的半径r=
| 1 |
| 2 |
∴球O的半径R=
12+(
|
∴球O的表面积S=4πR2=16π.
故选C.
.
点评:本题考查球的表面积的求法,合理地作出图形,数形结合求出球半径,是解题时要关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 (2012•洛阳模拟)阅读如图的算法框图,输出的结果S的值为( )
(2012•洛阳模拟)阅读如图的算法框图,输出的结果S的值为( )