题目内容
已知椭圆的中心在坐标原点O,焦点在坐标轴上,直线y=x+1与该椭圆相交于P和Q,且OP⊥OQ,|PQ|=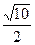 .求椭圆的方程.
.求椭圆的方程.
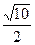 .求椭圆的方程.
.求椭圆的方程. , 或
, 或 
本小题考查椭圆的性质、两点的距离公式、两条直线垂直条件、二次方程根与系数的关系及分析问题的能力.满分12分.
解:求椭圆方程为
依题意知,点P、Q的坐标满足方程组
 将②式代入①式,整理得(a2+b2)x2+2a2x+a2(1-b2)="0, " ③ ——2分
将②式代入①式,整理得(a2+b2)x2+2a2x+a2(1-b2)="0, " ③ ——2分
设方程③的两个根分别为x1,x2,那么直线y=x+1与椭圆的交点为
P(x1,x1+1),Q(x2,x2+1). ——3分
由题设OP⊥OQ,|PQ|=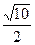 ,可得
,可得

整理得
 ——6分解这个方程组,得
——6分解这个方程组,得 或
或 
根据根与系数的关系,由③式得
(Ⅰ) 或 (Ⅱ)
或 (Ⅱ)  ——10分
——10分
解方程组(Ⅰ),(Ⅱ),得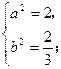 或
或 
故所求椭圆的方程为 , 或
, 或  ——12分
——12分
解:求椭圆方程为

依题意知,点P、Q的坐标满足方程组
|
 将②式代入①式,整理得(a2+b2)x2+2a2x+a2(1-b2)="0, " ③ ——2分
将②式代入①式,整理得(a2+b2)x2+2a2x+a2(1-b2)="0, " ③ ——2分设方程③的两个根分别为x1,x2,那么直线y=x+1与椭圆的交点为
P(x1,x1+1),Q(x2,x2+1). ——3分
由题设OP⊥OQ,|PQ|=
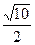 ,可得
,可得
整理得
|
 ——6分解这个方程组,得
——6分解这个方程组,得 或
或 
根据根与系数的关系,由③式得
(Ⅰ)
 或 (Ⅱ)
或 (Ⅱ)  ——10分
——10分解方程组(Ⅰ),(Ⅱ),得
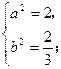 或
或 
故所求椭圆的方程为
 , 或
, 或  ——12分
——12分
练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
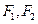 分别是椭圆
分别是椭圆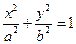 的左右焦点,
的左右焦点,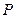 点在椭圆上,
点在椭圆上,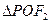 是面积为
是面积为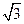 的正三角形,求
的正三角形,求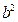 的值。
的值。 是椭圆
是椭圆 的两个焦点,
的两个焦点, 是椭圆上任意一点,求
是椭圆上任意一点,求 的最大值和最小值。
的最大值和最小值。 ,离心率
,离心率 ,那么它的短轴长是( )
,那么它的短轴长是( )

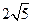

 ,
, ,若直线
,若直线 和椭圆
和椭圆 有公共点,则
有公共点,则 的取值范围是
的取值范围是
 、
、 ;
;  、
、 ;
;  、
、 ;
;  、
、 .
. 、
、 是它的焦点,长轴长为
是它的焦点,长轴长为 ,焦距为
,焦距为 ,静放在点
,静放在点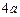
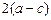

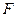 是椭圆的左焦点,
是椭圆的左焦点,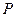 是椭圆上一点,
是椭圆上一点,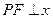 轴,
轴,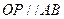 ,
, 求椭圆的离心率。
求椭圆的离心率。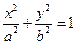 (
(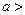
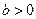 )的左、右焦点分别是
)的左、右焦点分别是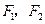 ,过
,过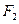 作倾斜角为
作倾斜角为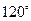 的直线与椭圆的一个交点为
的直线与椭圆的一个交点为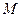 ,若
,若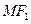 垂直于
垂直于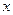 轴,则椭圆的离心率为( )
轴,则椭圆的离心率为( )