题目内容
18. 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°PA=PD=AD=2BC=2,$CD=\sqrt{3},PB=\sqrt{6}$,Q是AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°PA=PD=AD=2BC=2,$CD=\sqrt{3},PB=\sqrt{6}$,Q是AD的中点.(Ⅰ)求证:平面PQ⊥底面ABCD;
(Ⅱ)求三棱锥C-PBD的体积.
分析 (I)由PA=PD=AD=2,Q是AD的中点.可得PQ⊥AD,PQ=$\sqrt{3}$.连接QB,由底面ABCD为直角梯形,AD∥BC,∠ADC=90°,BC=QD,可得四边形BCDQ是矩形,BQ=$\sqrt{3}$.利用勾股定理的逆定理可得:PQ⊥QB,即可证明.
(II)由(I)可得:PQ⊥底面ABCD;可得:PQ是三棱锥P-BCD的底面BCD上的高.利用VC-PBD=VP-BCD=$\frac{1}{3}PQ•{S}_{△BCD}$即可得出.
解答 (I)证明:∵PA=PD=AD=2,Q是AD的中点.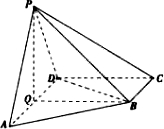
∴PQ⊥AD,PQ=$\sqrt{3}$.
连接QB,∵底面ABCD为直角梯形,AD∥BC,∠ADC=90°,BC=QD,
∴四边形BCDQ是矩形,∴BQ⊥AD,BQ=$\sqrt{3}$.
∴PQ2+QB2=PB2,
∴PQ⊥QB,
又AD∩QB=Q,
∴PQ⊥底面ABCD;
(II)解:由(I)可得:PQ⊥底面ABCD;
∴PQ是三棱锥P-BCD的底面BCD上的高.
S△BCD=$\frac{1}{2}BC•CD$=$\frac{1}{2}×1×\sqrt{3}$=$\frac{\sqrt{3}}{2}$,
∴VC-PBD=VP-BCD=$\frac{1}{3}PQ•{S}_{△BCD}$=$\frac{1}{3}×\sqrt{3}×\frac{\sqrt{3}}{2}$=$\frac{1}{2}$.
点评 本题考查了线面垂直的判定与性质定理、正三角形的性质、勾股定理的逆定理、矩形的性质、三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
8. 函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象的一部分如图所示,则此函数的解析式为( )
函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象的一部分如图所示,则此函数的解析式为( )
 函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象的一部分如图所示,则此函数的解析式为( )
函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象的一部分如图所示,则此函数的解析式为( )| A. | y=3sin($\frac{π}{4}$x+$\frac{π}{4}$) | B. | y=3sin($\frac{π}{4}$x+$\frac{3π}{4}$) | C. | y=3sin($\frac{π}{2}$x+$\frac{π}{4}$) | D. | y=3sin($\frac{π}{2}$x+$\frac{3π}{4}$) |
6.某几何体的三视图(单位:cm)如图,则这个几何体的体积为( )cm3.


| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $4\sqrt{3}$ | D. | $6\sqrt{3}$ |
13.已知复数z=$\frac{1}{-1+i}$(i为虚数单位),则z在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.已知复数z=1+i,则z2(1-z)=( )
| A. | 2 | B. | -2 | C. | 2-2i | D. | -2-2i |
 如图,射线OA,OB所在的直线的方向向量分别为$\overrightarrow{d_1}=({1,k})$,$\overrightarrow{d_2}=({1,-k})({k>0})$,点P在∠AOB内,PM⊥OA于M,PN⊥OB于N;
如图,射线OA,OB所在的直线的方向向量分别为$\overrightarrow{d_1}=({1,k})$,$\overrightarrow{d_2}=({1,-k})({k>0})$,点P在∠AOB内,PM⊥OA于M,PN⊥OB于N; 如图,在直三角形ABC-A1B1C1中,M为AB1的中点,△CMB1为等边三角形
如图,在直三角形ABC-A1B1C1中,M为AB1的中点,△CMB1为等边三角形