题目内容
(2013•重庆)对正整数n,记In={1,2,3…,n},Pn={ |m∈In,k∈In}.
|m∈In,k∈In}.
(1)求集合P7中元素的个数;
(2)若Pn的子集A中任意两个元素之和不是整数的平方,则称A为“稀疏集”.求n的最大值,使Pn能分成两个不相交的稀疏集的并.
(1)46 (2)n的最大值为14
解析

练习册系列答案
相关题目
若集合A={x|﹣2<x<1},B={x|0<x<2},则集合A∩B=( )
| A.{x|﹣1<x<1} | B.{x|﹣2<x<1} |
| C.{x|﹣2<x<2} | D.{x|0<x<1} |
已知全集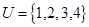 ,集合
,集合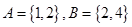 ,则
,则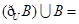
A. | B.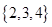 | C.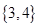 | D.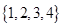 |
已知全集为R,集合M ={xlx2-2x-8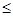 0),集合N={x|(1n2)l-x>1},则集合M
0),集合N={x|(1n2)l-x>1},则集合M (CRN)等于( )
(CRN)等于( )
| A.[-2,1] | B.(1,+ ) ) | C.[-l,4) | D.(1,4] |
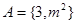 、
、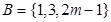 ,若
,若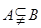 ,则实数
,则实数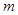 =___________.
=___________.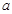 为实数,
为实数, :点
:点 在圆
在圆 的内部;
的内部;  :
: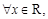 都有
都有 .
.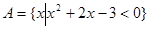 ,
,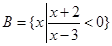 .
.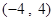 上任取一个实数
上任取一个实数 ,求“
,求“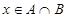 ”的概率;
”的概率;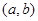 为有序实数对(如有序实数对(2,3)与(3,2)不一样),其中
为有序实数对(如有序实数对(2,3)与(3,2)不一样),其中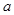 是从集合
是从集合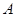 中任取的一个整数,
中任取的一个整数,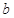 是从集合
是从集合 中任取的一个整数,求“
中任取的一个整数,求“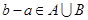 ”的概率
”的概率 ,则集合
,则集合 的个数为 .
的个数为 .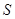 为复数集
为复数集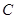 的非空子集.若对任意
的非空子集.若对任意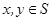 ,都有
,都有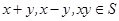 ,则称S为封闭集.下列命题:①集合S={a+bi|(
,则称S为封闭集.下列命题:①集合S={a+bi|(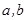 为整数,
为整数,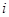 为虚数单位)}为封闭集;②若S为封闭集,则一定有
为虚数单位)}为封闭集;②若S为封闭集,则一定有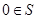 ;③封闭集一定是无限集;④若
;③封闭集一定是无限集;④若 的任意集合
的任意集合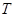 也是封闭集.其中真命题是 (写出所有真命题的序号).
也是封闭集.其中真命题是 (写出所有真命题的序号).