题目内容
已知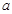 为实数,
为实数, :点
:点 在圆
在圆 的内部;
的内部;  :
: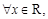 都有
都有 .
.
(1)若 为真命题,求
为真命题,求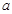 的取值范围;
的取值范围;
(2)若 为假命题,求
为假命题,求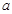 的取值范围;
的取值范围;
(3)若“ 且
且 ”为假命题,且“
”为假命题,且“ 或
或 ”为真命题,求
”为真命题,求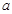 的取值范围.
的取值范围.
(1)  ;(2
;(2 )
) ;(3)
;(3)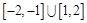 .
.
解析试题分析:(1)关键在于根据点与圆的位置关系的结论得到不等式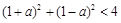 ;
;
(2)关键在于由一元二次函数,一元二次不等式,一元二次方程的知识可知,若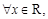 都有
都有 ,则对应的二次函数开口向上,二次方程的判别式
,则对应的二次函数开口向上,二次方程的判别式 ≤0;
≤0;
(3)由简易逻辑知识可知 与
与 一真一假,然后利用集合的运算和解不等式组知识即可解决.
一真一假,然后利用集合的运算和解不等式组知识即可解决.
试题解析:(1)由题意得,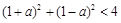 ,解得
,解得 ,
,
故 为真命题时
为真命题时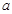 的取值范围为
的取值范围为 . 4分
. 4分
(2)若 为真命题,则
为真命题,则 ,解得
,解得 ,
,
故 为假命题时
为假命题时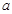 的取值范围
的取值范围 . 8分
. 8分
(3)由题意得, 与
与 一真一假,从而
一真一假,从而
当 真
真 假时有
假时有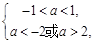 无解; 10分
无解; 10分
当 假
假 真时有
真时有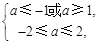 解得
解得 . 12分
. 12分
∴实数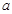 的取值范围是
的取值范围是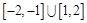 . 14分
. 14分
考点:(1) 点与圆的位置关系;(2)三个一元二次的关系;(3)简易逻辑;(4)集合的运算.

练习册系列答案
相关题目
设集合 ,集合
,集合 为函数
为函数 的定义域,则
的定义域,则 ( )
( )
A. | B. | C. | D.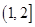 |
设集合U=R,集合M=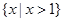 ,P=
,P=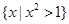 ,则下列关系正确的是( )
,则下列关系正确的是( )
| A.M=P | B.(CUM)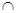 P= P=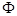 | C.P M M | D.M P P |
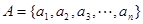 ,其中
,其中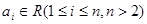 ,
,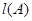 表示和
表示和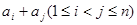 中所有不同值的个数.设集合
中所有不同值的个数.设集合 ,则
,则 .
. |m∈In,k∈In}.
|m∈In,k∈In}. ,集合
,集合 .
. ;
; ,求实数
,求实数 的取值范围.
的取值范围.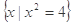 ,B=
,B=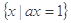 ,若B
,若B A,则实数
A,则实数 的取值集合为 .
的取值集合为 . 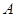 ,记
,记 .设非空实数集合
.设非空实数集合 ,若
,若 时,则
时,则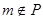 . 现给出以下命题:
. 现给出以下命题: ,必有
,必有 ;
;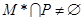 ;
; ;
;  ,使得对任意的
,使得对任意的 ,恒有
,恒有 ,
,