题目内容
(本题满分14分)
如图,已知 是棱长为
是棱长为 的正方体,点
的正方体,点 在
在 上,点
上,点 在
在 上,且
上,且 .
.
(1)求证: 四点共面;(4分)
四点共面;(4分)
(2)若点 在
在 上,
上,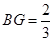 ,点
,点 在
在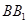 上,
上, ,垂足为
,垂足为 ,求证:
,求证: 平面
平面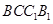 ;(4分)
;(4分)
(3)用 表示截面
表示截面 和侧面
和侧面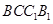 所成的锐二面角的大小,求
所成的锐二面角的大小,求 .(4分
.(4分

【答案】
(1)略
(2)略
(3)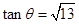 ;
;
【解析】(1)如图,在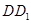 上取点
上取点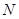 ,使
,使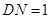 ,连结
,连结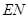 ,
,
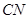 ,则
,则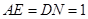 ,
,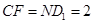 .
.
因为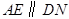 ,
,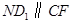 ,所以四边形
,所以四边形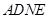 ,
,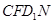 都为平行四边形.
都为平行四边形.
从而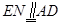 ,
,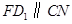 .
.
又因为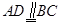 ,所以
,所以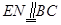 ,故四边形
,故四边形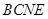 是平行四边形,
是平行四边形,
由此推知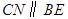 ,从而
,从而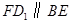 .
.
因此,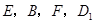 四点共面.
四点共面.
(2)如图,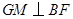 ,又
,又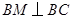 ,所以
,所以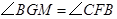 ,
,
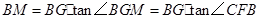
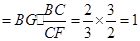 .
.
因为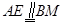 ,所以
,所以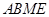 为平行四边形,从而
为平行四边形,从而 .
.
又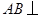 平面
平面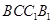 ,所以
,所以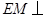 平面
平面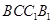 .
.
(3)如图,连结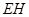
因为 ,
, ,
,
所以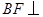 平面
平面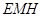 ,得
,得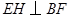 .
.
于是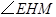 是所求的二面角的平面角,即
是所求的二面角的平面角,即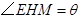 .
.
因为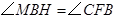 ,所以
,所以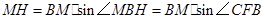
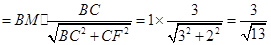 ,
,
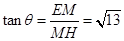 .
.
解法二:
(1)建立如图所示的坐标系,则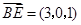 ,
,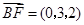 ,
,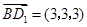 ,
,
所以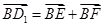 ,故
,故 ,
,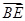 ,
,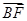 共面.
共面.
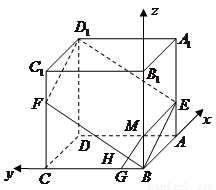 又它们有公共点
又它们有公共点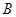 ,所以
,所以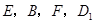 四点共面.
四点共面.
(2)如图,设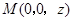 ,则
,则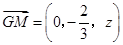 ,
,
而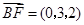 ,由题设得
,由题设得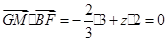 ,
,
得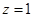 .
.
因为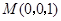 ,
,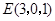 ,有
,有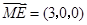 ,
,
又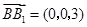 ,
,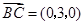 ,所以
,所以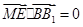 ,
,
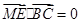 ,从而
,从而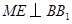 ,
,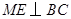 .
.
故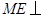 平面
平面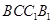 .
.
(3)设向量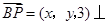 截面
截面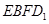 ,
,
于是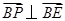 ,
,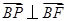 .
.
而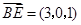 ,
,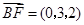 ,得
,得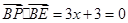 ,
,
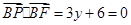 ,解得
,解得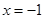 ,
,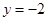 ,所以
,所以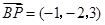 .
.
又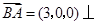 平面
平面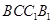 ,
,
所以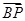 和
和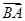 的夹角等于
的夹角等于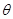 或
或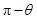 (
(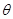 为锐角).
为锐角).
 于是
于是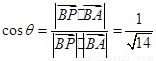 .
.
故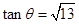 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 B=[0,3],求实数m的值
B=[0,3],求实数m的值 CRB,求实数m的取值范围
CRB,求实数m的取值范围 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。 ,在动点
,在动点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。 .
. 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使
 ).
).