题目内容
已知A、B是两个不同的点,m、n是两条不重合的直线,α、β是两个不重合的平面,则①m?α,A∈m⇒A∈α;②m∩n=A,A∈α,B∈m⇒B∈α;③m?α,m⊥β⇒α⊥β;④m?α,n?β,m∥n⇒α∥β.其中真命题为( )
分析:①m?α,A∈m⇒A∈α,可由点线面的位置关系判断;
②m∩n=A,A∈α,B∈m⇒B∈α,可由点线面的位置关系判断;
③m?α,m⊥β⇒α⊥β,可由线面垂直的判定判断;
④m?α,n?β,m∥n⇒α∥β,可由面面平行的判断方法判断.
②m∩n=A,A∈α,B∈m⇒B∈α,可由点线面的位置关系判断;
③m?α,m⊥β⇒α⊥β,可由线面垂直的判定判断;
④m?α,n?β,m∥n⇒α∥β,可由面面平行的判断方法判断.
解答:解:①m?α,A∈m⇒A∈α,此命题是正确命题,因为点在线上,线在面内,则点一定在面内;
②m∩n=A,A∈α,B∈m⇒B∈α,此命题不正确,因为本题中没有说明点B与面α的位置关系,故无法判断此点与面的位置关系;
③m?α,m⊥β⇒α⊥β,此命题正确,因为一个平面过另一个平面的垂线,由必垂直于这个平面;
④m?α,n?β,m∥n⇒α∥β,此命题不正确,两个平面中两两条线对应平行不能判断两个平面的位置关系,故不正确.
综上,①③是正确命题
故选A
②m∩n=A,A∈α,B∈m⇒B∈α,此命题不正确,因为本题中没有说明点B与面α的位置关系,故无法判断此点与面的位置关系;
③m?α,m⊥β⇒α⊥β,此命题正确,因为一个平面过另一个平面的垂线,由必垂直于这个平面;
④m?α,n?β,m∥n⇒α∥β,此命题不正确,两个平面中两两条线对应平行不能判断两个平面的位置关系,故不正确.
综上,①③是正确命题
故选A
点评:本题考查命题的真假判断与应用,解题的关键是掌握住空间中点线面位置的判断定理与性质以及有着较强的空间想像能力

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 ,
, 是两个不重合的平面,给出下列4个命题:①若
是两个不重合的平面,给出下列4个命题:①若 ,
, ,
, ,则
,则 ;②若
;②若 ,
, ,则
,则 ,则
,则 ;④若
;④若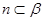 ,
, ,则
,则 ,其中真命题为( )
,其中真命题为( )