题目内容
已知A,B是两个不同的点,m,n是两条不重合的直线,α,β是两个不重合的平面,给出下列4个命题:
①若m∩n=A,A∈α,B∈m,则B∈α;
②若m?α,A∈m,则A∈α;
③若m?α,m⊥β,则α⊥β;
④若m?α,n?β,m∥n,则α∥β,
其中真命题为( )
①若m∩n=A,A∈α,B∈m,则B∈α;
②若m?α,A∈m,则A∈α;
③若m?α,m⊥β,则α⊥β;
④若m?α,n?β,m∥n,则α∥β,
其中真命题为( )
分析:根据空间点线面之间的关系,可判断①②;根据面面垂直的判定定理,可判断③;根据空间面面平行的位置关系及线线平行的位置关系,可判断④
解答:解:若m∩n=A,A∈α,B∈m,当m?α时,可得B∈α;当m∩α=A时,B∉α;故①为假命题;
若m?α,A∈m,则A∈α,故②为真命题
若m?α,m⊥β,则由面面垂直的判定定理得到α⊥β,故③为真命题;
若m?α,n?β,m∥n,则α与β可能平行也可能相交,故④为假命题;
其中真命题为②③
故选C
若m?α,A∈m,则A∈α,故②为真命题
若m?α,m⊥β,则由面面垂直的判定定理得到α⊥β,故③为真命题;
若m?α,n?β,m∥n,则α与β可能平行也可能相交,故④为假命题;
其中真命题为②③
故选C
点评:本题以命题的真假判断为载体考查了空间直线与平面之间的位置关系,平面与平面之间的位置关系,难度不大,属于基础题目

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 ,
, 是两个不重合的平面,给出下列4个命题:①若
是两个不重合的平面,给出下列4个命题:①若 ,
, ,
, ,则
,则 ;②若
;②若 ,
, ,则
,则 ,则
,则 ;④若
;④若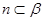 ,
, ,则
,则 ,其中真命题为( )
,其中真命题为( )