题目内容
已知A、B是两个不同的点,m、n是两条不重合的直线,α、β是两个不重合的平面,则①m?α,A∈m?A∈α;②m∩n=A,A∈α,B∈m?B∈α;③m?α,n?β,m∥n?α∥β;④m?α,m⊥β?α⊥β.其中真命题为( )
| A.①③ | B.①④ | C.②③ | D.②④ |
对于①,根据平面的基本性质,可得结论A∈α,故①正确;
对于②,点B可能在α内,也可能在平面α外,故②不正确;
对于③,根据面面平行的判定定理,不能得出α∥β,故③不正确;
对于④,m?α,m⊥β,则利用面面平行的判定,可得α⊥β.④正确.
其中真命题为①④.
故选B.
对于②,点B可能在α内,也可能在平面α外,故②不正确;
对于③,根据面面平行的判定定理,不能得出α∥β,故③不正确;
对于④,m?α,m⊥β,则利用面面平行的判定,可得α⊥β.④正确.
其中真命题为①④.
故选B.

练习册系列答案
相关题目
 ,
, 是两个不重合的平面,给出下列4个命题:①若
是两个不重合的平面,给出下列4个命题:①若 ,
, ,
, ,则
,则 ;②若
;②若 ,
, ,则
,则 ,则
,则 ;④若
;④若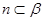 ,
, ,则
,则 ,其中真命题为( )
,其中真命题为( )