题目内容
设a,b,c,d∈R,若a,1,b成等比数列,且c,1,d 成等差数列,则下列不等式恒成立的是( )A.a+b≤2cd
B.a+b≥2cd
C.|a+b|≤2cd
D.|a+b|≥2cd
【答案】分析:由题意可得ab=1,c+d=2,由于a,b,c,d的正负不确定,选项A,B不恒成立,由于ab=1>0,则a,b同号,|a+b|=|a|+|b|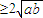 =2,当cd<0时,c+d>0>2cd;当cd>0时,由c+d=2可知,c>0,d>0,则可知cd
=2,当cd<0时,c+d>0>2cd;当cd>0时,由c+d=2可知,c>0,d>0,则可知cd =1,从而可得
=1,从而可得
解答:解:由题意可得ab=1,c+d=2
由于a,b,c,d的正负不确定
A:例如a=-2,b=- ,c=-8,d=10,此时a+b>2cd,故A错误
,c=-8,d=10,此时a+b>2cd,故A错误
B:例如a=-2,b=- ,c=1,d=1,此时a+b<2cd,故B错误
,c=1,d=1,此时a+b<2cd,故B错误
由于ab=1>0,则a,b同号,|a+b|=|a|+|b|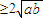 =2,
=2,
当cd<0时,c+d>0>2cd
当cd>0时,由c+d=2可知,c>0,d>0,则可知cd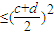 =1
=1
∴|a+b|≥2cd
综上可得,|a+b|≥2cd
点评:本题主要考查了基本不等式的灵活应用,解题的关键是判断基本不等式的应用条件,解题中要注意对各种情况都要考虑
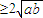 =2,当cd<0时,c+d>0>2cd;当cd>0时,由c+d=2可知,c>0,d>0,则可知cd
=2,当cd<0时,c+d>0>2cd;当cd>0时,由c+d=2可知,c>0,d>0,则可知cd =1,从而可得
=1,从而可得解答:解:由题意可得ab=1,c+d=2
由于a,b,c,d的正负不确定
A:例如a=-2,b=-
 ,c=-8,d=10,此时a+b>2cd,故A错误
,c=-8,d=10,此时a+b>2cd,故A错误B:例如a=-2,b=-
 ,c=1,d=1,此时a+b<2cd,故B错误
,c=1,d=1,此时a+b<2cd,故B错误由于ab=1>0,则a,b同号,|a+b|=|a|+|b|
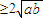 =2,
=2,当cd<0时,c+d>0>2cd
当cd>0时,由c+d=2可知,c>0,d>0,则可知cd
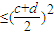 =1
=1∴|a+b|≥2cd
综上可得,|a+b|≥2cd
点评:本题主要考查了基本不等式的灵活应用,解题的关键是判断基本不等式的应用条件,解题中要注意对各种情况都要考虑

练习册系列答案
相关题目
设a、b、c、d∈R,且ab>0,-
<-
,则以下不等式成立的是( ).
| c |
| a |
| d |
| b |
| A、bc<ad | ||||
B、
| ||||
| C、bc>ad | ||||
D、
|
设a,b,c,d∈R.且a>b,c>d,且下列结论中正确的是( )
| A、a+c>b+d | ||||
| B、a-c>b-d | ||||
| C、ac>bd | ||||
D、
|
设a,b,c,d∈R,则条件甲:ac=2(b+d)是条件乙:方程x2+ax+b=0与方程x2+cx+d=0中至少有一个有实根的( )
| A、充分而不必要条件 | B、必要而不充分条件 | C、充要条件 | D、既不充分也不必要条件 |