��Ŀ����
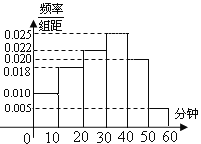
����Ŀ��������ȫ����һ�����߳��д��Ͷ��������½����̨��ס������.ij��Ϊ�˽�һ���˽��ѹ������ڶ���������̨¥���������ͬ����������ȡ��һС��ס�����е���,�����˾�������(��λ��ǧԪ)��Ƶ���ֲ�����¥������Ļ������±���
�˾������� |
|
|
|
|
|
|
Ƶ�� | 6 | 10 | 13 | 11 | 8 | 2 |
�ɻ��� | 5 | 9 | 12 | 9 | 4 | 1 |
����С���˾������벻����7.5ǧԪ��ס����Ϊ�������뻧��,�˾����������7.5ǧԪ��ס����Ϊ���Ǹ����뻧��
�Ǹ����뻧 | �����뻧 | �ܼ� | |
�� | |||
���� | |||
�ܼ� |
�����Ǹ����뻧���ڱ��γ��������е���ռ������
�����ִ���������![]() ��ס���������ȡ������������ȡ����������¥������ĸ��ʣ�
��ס���������ȡ������������ȡ����������¥������ĸ��ʣ�
������������֪���������ͼ������![]() ����������˵���ܷ��ڷ�����ĸ��ʲ�����0.005��ǰ������Ϊ������ĸߵ͡��롰��¥������й�.
����������˵���ܷ��ڷ�����ĸ��ʲ�����0.005��ǰ������Ϊ������ĸߵ͡��롰��¥������й�.
�����ٽ�ֵ��
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�ο���ʽ��  ��
�� ![]() .
.
���𰸡���1��![]() ��2��
��2��![]() ��3������
��3������
�������������������1������Ƶ���������ı�ֵ�á��Ǹ����뻧�����γ��������е���ռ��������2���˾���������![]() ��,��5����¥������, l������¥���������ö�ٷ�ȷ�����������ȡ�������еĻ�ľ�¼�������ȷ������ȡ����������¥����������Ļ����¼����������ݹŵ�����ʹ�ʽ����ʣ���3�����ݿ�����ʽ��
��,��5����¥������, l������¥���������ö�ٷ�ȷ�����������ȡ�������еĻ�ľ�¼�������ȷ������ȡ����������¥����������Ļ����¼����������ݹŵ�����ʹ�ʽ����ʣ���3�����ݿ�����ʽ��![]() ����ο����ݱȽϣ�ȷ������.
����ο����ݱȽϣ�ȷ������.
���������������Ϊ![]() ��
��
���ԡ��Ǹ����뻧�����γ��������е���ռ����Ϊ![]() .
.
�����˾���������![]() ��,��5����¥������,�ֱ��Ϊ
��,��5����¥������,�ֱ��Ϊ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ,
,![]() ��l������¥�������Ϊ
��l������¥�������Ϊ![]() .
.
�ִ��������ȡ���������еĻ�ľ�¼��У� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ����15����
����15����
�¼�������ȡ����������¥����������Ļ����¼��У� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ����10����
����10����
������ȡ����������¥������ĸ���Ϊ![]() .
.
�����������⣬�ɵ�����![]() ��������
��������
�Ǹ������� | �������� | �ܼ� | |
�� | 35 | 5 | 40 |
���� | 5 | 5 | 10 |
�ܼ� | 40 | 10 | 50 |
��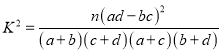
![]() ��
��
����ڷ�����ĸ��ʲ�����0.005��ǰ������Ϊ������ĸߵ͡��롰��¥������й�.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ij��ѧѧ����Ϊ�˵��鰮����Ӿ�˶����Ա��Ƿ��йأ�ͨ�����ѯ��110���Ա�ͬ�ĸ������Ƿ���Ӿ�˶��õ����µ���������
p��k2��k�� | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
�� | Ů | �ܼ� | |
���� | 40 | 20 | 60 |
������ | 20 | 30 | 50 |
�ܼ� | 60 | 50 | 110 |
��![]() �������ո������õ�����ȷ�����ǣ�������
�������ո������õ�����ȷ�����ǣ�������
A. �ڷ�����ĸ��ʲ�����![]() ��ǰ���£���Ϊ��������Ӿ�˶����Ա��йء�
��ǰ���£���Ϊ��������Ӿ�˶����Ա��йء�
B. �ڷ�����ĸ��ʲ�����![]() ��ǰ���£���Ϊ��������Ӿ�˶����Ա��ء�
��ǰ���£���Ϊ��������Ӿ�˶����Ա��ء�
C. ��![]() �İ�����Ϊ��������Ӿ�˶����Ա��йء�
�İ�����Ϊ��������Ӿ�˶����Ա��йء�
D. ��![]() �İ�����Ϊ��������Ӿ�˶����Ա��ء�
�İ�����Ϊ��������Ӿ�˶����Ա��ء�