题目内容
已知函数
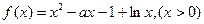
(1)当
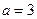 时,求
时,求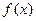 的单调递增区间;
的单调递增区间;(2)若
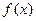 在
在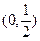 上是增函数,求
上是增函数,求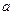 的取值范围;
的取值范围;(3)是否存在实数
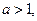 使得方程
使得方程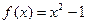 在区间
在区间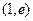 上有解,若存在,
上有解,若存在,试求出
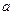 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由. (1)
 单调增区间为
单调增区间为
(2)

(3)不存在
解:(1)当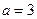 时,
时,
 ,解得
,解得 或
或 ,又
,又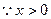
 单调增区间为
单调增区间为
(2)若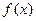 在
在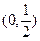 上是增函数,则对任意
上是增函数,则对任意 ,
, 恒成立,
恒成立,
 等价于:
等价于:
 ,
, 恒成立,等价于:
恒成立,等价于:
 恒成立
恒成立
令 ,
,
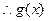 在
在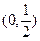 上为减函数,
上为减函数,
(3)假设 方程
方程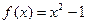 在区间
在区间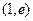 有解,等价转化为:
有解,等价转化为:
当 函数
函数 在区间
在区间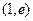 上有零点
上有零点
令 解得:
解得: ,又
,又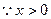 ,
, 单调增区间为
单调增区间为 ,单调减区间
,单调减区间 ,
, ,
, 在
在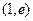 上为减区间,而
上为减区间,而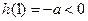 ,
,
故 在
在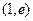 上不存在零点
上不存在零点
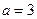 时,
时,
 ,解得
,解得 或
或 ,又
,又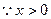
 单调增区间为
单调增区间为
(2)若
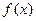 在
在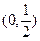 上是增函数,则对任意
上是增函数,则对任意 ,
, 恒成立,
恒成立, 等价于:
等价于: ,
, 恒成立,等价于:
恒成立,等价于:
 恒成立
恒成立令
 ,
,
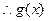 在
在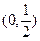 上为减函数,
上为减函数,
(3)假设
 方程
方程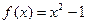 在区间
在区间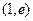 有解,等价转化为:
有解,等价转化为:当
 函数
函数 在区间
在区间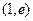 上有零点
上有零点令
 解得:
解得: ,又
,又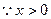 ,
, 单调增区间为
单调增区间为 ,单调减区间
,单调减区间 ,
, ,
, 在
在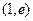 上为减区间,而
上为减区间,而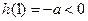 ,
,故
 在
在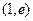 上不存在零点
上不存在零点
练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
 和“伪二次函数”
和“伪二次函数”
 (
( 、
、 、
、
 ),
), ,无论
,无论 在定义域内不可能总为增函数;
在定义域内不可能总为增函数; ,线段
,线段 中点的横坐标为
中点的横坐标为 ,记直线
,记直线 ,
,  i)求证:
i)求证: ;
; ,是否有(i)同样的性质?证明你的结论.
,是否有(i)同样的性质?证明你的结论. 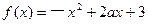 ,
,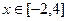
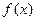 的最大值关于
的最大值关于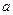 的解析式
的解析式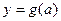
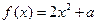 ,且
,且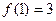 .(I)求
.(I)求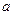 的值;(II)求函数
的值;(II)求函数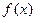 在[1,3]上的最小值和最大值.
在[1,3]上的最小值和最大值. 在
在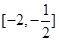 上单调递增,那么
上单调递增,那么 的取值范围是( )
的取值范围是( )



 本题满分15分)
本题满分15分) 数
数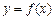 满足:当
满足:当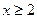 时,
时,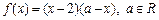 ,当
,当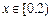 时,
时,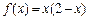
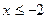 时,
时,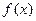 的表达式;
的表达式;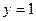 与函数
与函数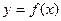 的图象恰好有两个公共点,求实数
的图象恰好有两个公共点,求实数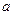 的取值范围。
的取值范围。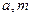 满足什么条件时,函数
满足什么条件时,函数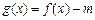 有4个零点且这4个零点从小到大依次成等差数列。
有4个零点且这4个零点从小到大依次成等差数列。

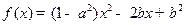 (
(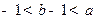 ). 用
). 用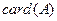 表示集合
表示集合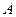 中元素的个数,若使得
中元素的个数,若使得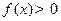 成立的充分必要条件是
成立的充分必要条件是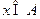 ,且
,且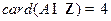 ,则实数
,则实数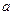 的取值范围是( )
的取值范围是( )



 ,如果
,如果 (其中
(其中 ),则
),则 ( )
( )