题目内容
设P是椭圆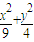
=1上一点，F1、F2是椭圆的两个焦点，则cos∠F1PF2的最小值是（ ）A．-
B．-1
C．
D．
【答案】分析：利用椭圆的定义，余弦定理，结合基本不等式，即可求cos∠F1PF2的最小值是
解答：解：由题意，|PF1|+|PF2|=6，|F1F2|=2
∴cos∠F1PF2=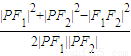
=
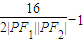
∵|PF1|+|PF2|=6≥2
∴2|PF1||PF2|≤9
∴
≥
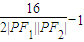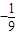
故选A．
点评：本题考查椭圆的定义，余弦定理，考查基本不等式，属于基础题．
解答：解：由题意，|PF1|+|PF2|=6，|F1F2|=2
∴cos∠F1PF2=
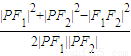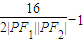
=∵|PF1|+|PF2|=6≥2
∴2|PF1||PF2|≤9
∴
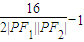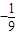
≥故选A．
点评：本题考查椭圆的定义，余弦定理，考查基本不等式，属于基础题．
练习册系列答案
相关题目
=1上一点，P到两焦点F1、F2的距离之差为2，则△PF1F2是( ) 
=1上一点,P到两焦点F1、F2的距离之差为2,则△PF1F2是
+
=1上一点,F1、F2是椭圆的两个焦点,则cos∠F1PF2的最小值是
B.－
D.
+
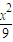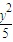=1上一点，M，N分别是两圆：（x+2）2+y2=1和（x-2）2+y2=1上的点，则|PM|+|PN|的最小值、最大值分别为（ ）