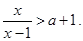题目内容
(本题满分12分)
已知函数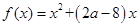 ,不等式
,不等式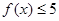 的解集是
的解集是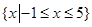 .
.
(1)求实数 的值;
的值;
(2) 对于
对于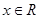 恒成立,求实数
恒成立,求实数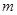 的取值范围.
的取值范围.
(1) ;
;
(2) 的单调递增区间是
的单调递增区间是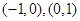 ,单调递减区间是
,单调递减区间是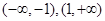 .(12分)
.(12分)
解析试题分析:(1)根据二次函数的不等式的解集,结合韦达定理可知参数a,b的值,求解解析式。
(2)要使得不等式 对于
对于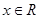 恒成立,,只要求解函数f(x)的最小值即可。转化与划归思想的运用。
恒成立,,只要求解函数f(x)的最小值即可。转化与划归思想的运用。
解(1)设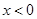 ,则
,则 ,
,
所以 (3分)
(3分)
又 是
是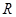 上的奇函数,则
上的奇函数,则 ,
, (4分)
(4分)
所以, (6分)
(6分)
(2)函数 的图像略
的图像略
(画图像关键点必须画准确,如顶点、端点、点的虚实,变化趋势等9分)
根据函数 的图像可知,
的图像可知, 的单调递增区间是
的单调递增区间是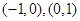 ,
,
单调递减区间是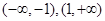 .(12分)
.(12分)
考点:本题主要考查了一元二次不等式的应用,二次函数性质的运用。体现了分类讨论的数学思想.
点评:解决该试题的关键是能结合不等式的解集得到参数的取值进而得到解析式,而对于恒成立的问题,通常转化为最大值或者最小值问题来处理即可。

练习册系列答案
相关题目
设二次函数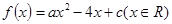 的值域为[0,+∞),则
的值域为[0,+∞),则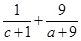 的最大值是( )
的最大值是( )
A.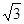 | B.2 | C.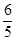 | D.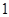 |
设x>0,y>0,且x+4y=40,则lgx+lgy的最大值是( )
| A.40 | B.10 | C.4 | D.2 |
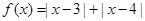 .
.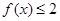 ;
;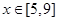 ,
,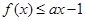 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. .
.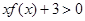 ;
;  ,不等式
,不等式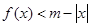 恒成立,求
恒成立,求 的取值范围.
的取值范围.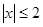 ,
,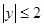 ,点
,点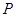 的坐标为
的坐标为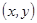
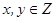 时,求
时,求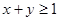 的概率。
的概率。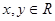 时,求
时,求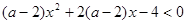 对一切
对一切 恒成立,试确定实数
恒成立,试确定实数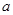 的取值范围.
的取值范围.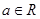 ,解不等式
,解不等式