题目内容
9. 如图,已知PA与半圆O切于点A,PO交半圆O于点B、C,AD⊥PO于点D.
如图,已知PA与半圆O切于点A,PO交半圆O于点B、C,AD⊥PO于点D.(Ⅰ)求证AB平分∠PAD;
(Ⅱ)求证$\frac{PB}{PC}=\frac{DB}{DC}$.
分析 (Ⅰ)利用BC为半圆O的直径,AD⊥BC,PA与半圆O切于点A,证明∠PAB=∠BAD,即可证明AB平分∠PAD;
(Ⅱ)证明△PAB∽△PCA,$\frac{PB}{BD}$=$\frac{PC}{CD}$,即可证明$\frac{PB}{PC}=\frac{DB}{DC}$.
解答 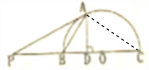 证明:(Ⅰ)由题意,BC为半圆O的直径,A为半圆O上一点,
证明:(Ⅰ)由题意,BC为半圆O的直径,A为半圆O上一点,
∴∠BAC=90°,
∵AD⊥BC,
∴∠BAD=∠ACD,
∵PA与半圆O切于点A,
∴∠PAB=∠ACD,
∴∠PAB=∠BAD,
∴AB平分∠PAD;
(Ⅱ)连接AC,
∵∠PAB=∠PCA,∠P=∠P,
∴△PAB∽△PCA,
∴$\frac{PA}{PC}=\frac{PB}{PA}=\frac{AB}{AC}$.
在Rt△BAC中,AD⊥CD,
∴$\frac{AB}{AC}=\frac{AD}{CD}=\frac{BD}{AD}$,
∴$\frac{PA}{PC}=\frac{AD}{CD}$,$\frac{PB}{PA}$=$\frac{BD}{AD}$,
∴$\frac{PC}{DC}=\frac{PA}{AD}$,$\frac{PB}{BD}$=$\frac{PA}{AD}$,
∴$\frac{PB}{BD}$=$\frac{PC}{CD}$,
∴$\frac{PB}{PC}=\frac{DB}{DC}$.
点评 本题考查圆的切线的性质,考查三角形相似的判定与性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
17.若满足条件AB=2且B=60°的三角形有两个,则AC边长的取值范围是( )
| A. | (1,2) | B. | ($\sqrt{2}$,$\sqrt{3}$) | C. | ($\sqrt{3}$,2) | D. | ($\sqrt{2}$,2) |
4.等比数列{an}满足a2+8a5=0,设数列{$\frac{1}{{a}_{n}}$}的前n项和为Sn,则$\frac{{S}_{5}}{{S}_{2}}$=( )
| A. | -11 | B. | -8 | C. | 5 | D. | 11 |
1.已知等比数列{an}的公比q=2,前n项和为Sn,若S4=1,则S8=( )
| A. | 15 | B. | 17 | C. | 19 | D. | 21 |