题目内容
【题目】在矩形ABCD中,AB=1,AD=2,△ABD沿对角线BD翻折,形成三棱锥A﹣BCD.
①当![]() 时,三棱锥A﹣BCD的体积为
时,三棱锥A﹣BCD的体积为![]() ;
;
②当面ABD⊥面BCD时,AB⊥CD;
③三棱锥A﹣BCD外接球的表面积为定值.
以上命题正确的是_____.
【答案】③
【解析】
在①中,由题意可得![]() 平面ACD,利用
平面ACD,利用![]() 即能求出三棱锥A﹣BCD的体积;在②中,过点A作AE⊥平面BCD,交BD于E,则AE⊥CD,即可得 AB与CD不垂直;在③中,三棱锥A﹣BCD外接球的球心为O,半径为
即能求出三棱锥A﹣BCD的体积;在②中,过点A作AE⊥平面BCD,交BD于E,则AE⊥CD,即可得 AB与CD不垂直;在③中,三棱锥A﹣BCD外接球的球心为O,半径为![]() ,从而三棱锥A﹣BCD外接球的表面积为定值.
,从而三棱锥A﹣BCD外接球的表面积为定值.
∵在矩形ABCD中,AB=1,AD=2,
∴AC=BD![]() ,
,
△ABD沿对角线BD翻折,形成三棱锥A﹣BCD.
在①中,当![]() 时,
时, ![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
又![]() ,∴
,∴![]() 平面ACD,
平面ACD,
∴![]() ,故①错误;
,故①错误;
在②中,当面ABD⊥面BCD时,过点A作AE⊥平面BCD,交BD于E,
则AE⊥CD,又CD与平面ABD不垂直,故AB与CD不垂直,故②错误;
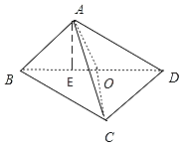
在③中,取BD的中点O,连接OA、OC,
∵OA=OB=OC=OD![]() ,
,
∴三棱锥A﹣BCD外接球的球心为O,半径为![]() ,
,
∴三棱锥A﹣BCD外接球的表面积为定值,故③正确.
故答案为:③.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目