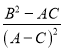Question

【题目】已知函数.

(1)求函数的最小正周期并求出单调递增区间;

(2)在中,角A,B,C的对边分别是a,b,c,且满足,求的取值范围.

Answer 1

【答案】(1)的最小正周期为;递增区间为()(2)

【解析】

(1)利用正弦的二倍角公式和降幂公式将函数的解析式化为的形式,然后求出函数的最小正周期,再计算得到函数的单调递增区间.

(2)运用余弦定理对已知条件进行化简,求出角的值,计算出角的取值范围,代入(1)中化简得到的解析式中,分步求解出的取值范围.

(1)已知函数,化简得

,

即,所以函数的最小正周期为,代入函数的单调增区间求得(),

解得().

综上的最小正周期为;递增区间为()

(2)由余弦定理得,代入得,化简得,又,所以,则,

,又,则,

,,,即,综上的取值范围为.