题目内容
已知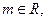 且复数z=(2+
且复数z=(2+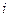 )
)
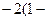
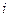 )在复平面内表示的点为A.
)在复平面内表示的点为A.
(1)当实数m取什么值时,复数z是纯虚数;
(2)当点A位于第二象限时,求实数m的取值范围.
(1)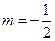
(2)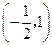
解析

练习册系列答案
相关题目
设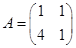 ,则矩阵
,则矩阵 的一个特征值
的一个特征值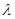 和对应的一个特征向量
和对应的一个特征向量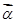 为
为
A. , , | B.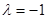 , ,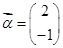 |
C. , , | D.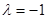 , , |
题目内容
已知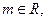 且复数z=(2+
且复数z=(2+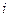 )
)
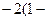
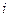 )在复平面内表示的点为A.
)在复平面内表示的点为A.
(1)当实数m取什么值时,复数z是纯虚数;
(2)当点A位于第二象限时,求实数m的取值范围.
(1)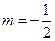
(2)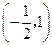
解析

设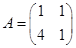 ,则矩阵
,则矩阵 的一个特征值
的一个特征值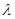 和对应的一个特征向量
和对应的一个特征向量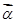 为
为
A. , , | B.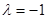 , ,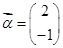 |
C. , , | D.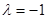 , , |