Question

集合A＝{x|－2≤x≤5}，集合B＝{x|m＋1≤x≤2m－1}．　

(1) 若B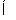A，求实数m的取值范围；

(2) 当x∈R时，没有元素x使x∈A与x∈B同时成立，求实数m的取值范围．

 

Answer 1

（1）m≤3（2）m＜2或m＞4

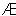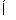【解析】(1) 当m＋1＞2m－1即m＜2时，B＝满足BA；

当m＋1≤2m－1即m≥2时，要使B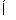A成立，则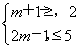解得2≤m≤3.

综上所述，当m≤3时有B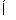A.

(2) 因为x∈R，且A＝{x|－2≤x≤5}，B＝{x|m＋1≤x≤2m－1}，又没有元素x使x∈A与x∈B同时成立，则

① 若B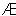＝，即m＋1＞2m－1，得m＜2时满足条件；

② 若B≠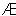，则要满足条件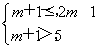解得m＞4.

或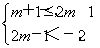无解．

综上所述，实数m的取值范围为m＜2或m＞4