题目内容
 已知在空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别是BC、CD上的点,且BG:GC=DH:HC=2:1,则EG、FH、AC的位置关系是
已知在空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别是BC、CD上的点,且BG:GC=DH:HC=2:1,则EG、FH、AC的位置关系是
- A.两两异面
- B.两两平行
- C.交于一点
- D.两两相交
C
分析:由题意连接EF、HG、GE、FH、AC,根据比例关系和中位线证明出四边形EFHG是梯形,则两腰和底边上的中线一定相交于一点.
解答: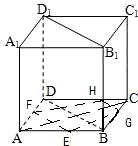 解:连接EF、HG、GE、FH、AC,如图:
解:连接EF、HG、GE、FH、AC,如图:
∵BG:GC=DH:HC=2:1,
∴HG∥DB,且HG= BD,
BD,
∵E、F分别是AB、AD的中点,
∴EF∥BD,且EF= BD,
BD,
∴四边形EFHG是梯形,
∵AC是底边上的中线,
∴EG、FH、AC相交于一点.
故选C.
点评:本题考查了线线平行关系,主要根据平面几何中比例关系和中位线来证明线线平行,即平面几何中的知识在空间几何的一个平面内仍然适用.
分析:由题意连接EF、HG、GE、FH、AC,根据比例关系和中位线证明出四边形EFHG是梯形,则两腰和底边上的中线一定相交于一点.
解答:
 解:连接EF、HG、GE、FH、AC,如图:
解:连接EF、HG、GE、FH、AC,如图:∵BG:GC=DH:HC=2:1,
∴HG∥DB,且HG=
 BD,
BD,∵E、F分别是AB、AD的中点,
∴EF∥BD,且EF=
 BD,
BD,∴四边形EFHG是梯形,
∵AC是底边上的中线,
∴EG、FH、AC相交于一点.
故选C.
点评:本题考查了线线平行关系,主要根据平面几何中比例关系和中位线来证明线线平行,即平面几何中的知识在空间几何的一个平面内仍然适用.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
 已知在空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别是BC、CD上的点,且BG:GC=DH:HC=2:1,则EG、FH、AC的位置关系是( )
已知在空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别是BC、CD上的点,且BG:GC=DH:HC=2:1,则EG、FH、AC的位置关系是( )| A、两两异面 | B、两两平行 | C、交于一点 | D、两两相交 |
 (2011•顺义区一模)如图,已知在空间四边形ABCD中,AB=AC=DB=DC,E为BC的中点.
(2011•顺义区一模)如图,已知在空间四边形ABCD中,AB=AC=DB=DC,E为BC的中点.
