题目内容
已知函数 .
.
(1)若函数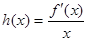 为奇函数,求a的值;
为奇函数,求a的值;
(2)若函数 在
在 处取得极大值,求实数a的值;
处取得极大值,求实数a的值;
(3)若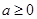 ,求
,求 在区间
在区间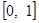 上的最大值.
上的最大值.
(1)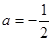 ;(2)
;(2)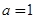 ;(3) 当
;(3) 当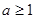 时,
时, 在
在 取得最大值
取得最大值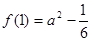 ;
;
当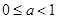 时,
时,  取得最大值
取得最大值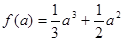 .
.
解析试题分析:(1)首先求出导数: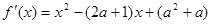 ,
,
代入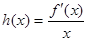 得:
得: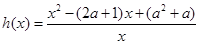 .
.
因为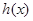 为奇函数,所以
为奇函数,所以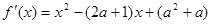 必为偶函数,即
必为偶函数,即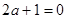 ,
,
所以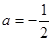 .
.
(2)首先求出函数的极大值点.又由题设:函数 在
在 处取得极大值.二者相等,便可得
处取得极大值.二者相等,便可得 的值.
的值.
(3)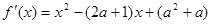
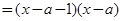 .
.
由 得:
得: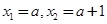 .
.
注意它的两个零点的差恰好为1,且必有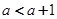 .
.
结合导函数的图象,可知导函数的符号,从而得到函数 的单调区间和极值点.
的单调区间和极值点.
试题解析:(1)因为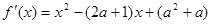 ,
,
所以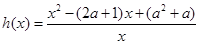 2分
2分
由二次函数奇偶性的定义,因为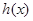 为奇函数,
为奇函数,
所以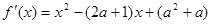 为偶函数,即
为偶函数,即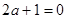 ,
,
所以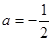 4分
4分
(2)因为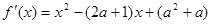
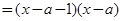 .
.
令 ,得
,得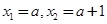 ,显然
,显然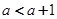 .
.
所以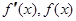 随
随 的变化情况如下表:
的变化情况如下表:
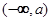

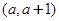
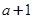

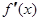
+ 0 - 0 + 
递增  练习册系列答案
练习册系列答案
新编高中同步作业系列答案
同步AB卷高效考卷系列答案
考易百分百周末提优训练系列答案
南粤学典学考精练系列答案
全优期末测评系列答案
学习与巩固系列答案
B卷狂练系列答案
易考100一考通系列答案
伴你学系列答案
启航新课堂系列答案
相关题目
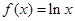 ,
,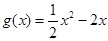 .
.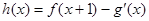 (其中
(其中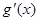 是
是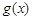 的导函数),求
的导函数),求 的最大值;
的最大值;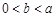 时,有
时,有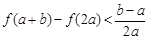 ;
;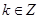 ,当
,当 时,不等式
时,不等式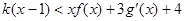 恒成立,求
恒成立,求 的最大值.
的最大值.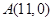 ,函数
,函数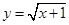 的图象上的动点
的图象上的动点 在
在 轴上的射影为
轴上的射影为 ,且点
,且点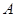 的左侧.设
的左侧.设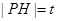 ,
,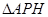 的面积为
的面积为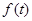 .
.
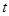 的取值范围;
的取值范围;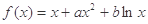 ,曲线
,曲线 过点P(1,0),且在P点处的切斜线率为2.
过点P(1,0),且在P点处的切斜线率为2.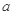 ,
,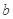 的值;
的值;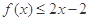 .
.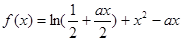
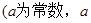 >0)
>0) 的一个极值点,求
的一个极值点,求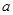 的值;
的值;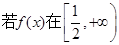 上是增函数,求a的取值范围
上是增函数,求a的取值范围 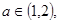 总存在
总存在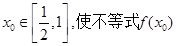 >
>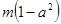 成立,求实数m的取值范围
成立,求实数m的取值范围 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式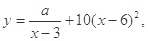 其中
其中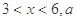 为常数.己知销售价格为5元/千克时,每日可售出该商品11千克.
为常数.己知销售价格为5元/千克时,每日可售出该商品11千克. 的值;
的值;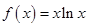 .
.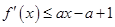 恒成立,求实数a的集合.
恒成立,求实数a的集合.
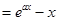 ,其中
,其中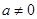 .
.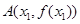 ,
,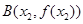
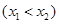 ,记直线AB的斜率 为k,问:是否存在x0∈(x1,x2),使
,记直线AB的斜率 为k,问:是否存在x0∈(x1,x2),使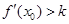 成立?若存在,求
成立?若存在,求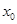 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.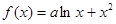 (
( 为实常数)
为实常数) 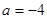 时,求函数
时,求函数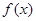 在
在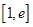 上的最大值及相应的
上的最大值及相应的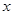 值;
值;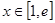 时,讨论方程
时,讨论方程 根的个数
根的个数 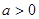 ,且对任意的
,且对任意的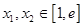 ,都有
,都有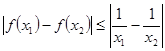 ,求实数a的取值范围
,求实数a的取值范围