题目内容
如图,已知点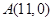 ,函数
,函数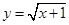 的图象上的动点
的图象上的动点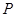 在
在 轴上的射影为
轴上的射影为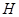 ,且点
,且点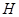 在点
在点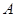 的左侧.设
的左侧.设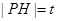 ,
,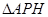 的面积为
的面积为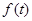 .
.
(Ⅰ)求函数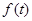 的解析式及
的解析式及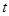 的取值范围;
的取值范围;
(Ⅱ)求函数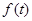 的最大值.
的最大值.
(Ⅰ)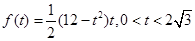 .
.
(Ⅱ)当 时,函数
时,函数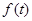 取得最大值8.
取得最大值8.
解析试题分析:(Ⅰ)确定三角形面积,主要确定底和高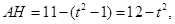 .
.
(Ⅱ)应用导数研究函数的最值,遵循“求导数,求驻点,讨论驻点两侧导数正负,比较极值与区间端点函数值”.利用“表解法”形象直观,易以理解.
试题解析:(Ⅰ)由已知可得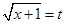 ,所以点
,所以点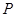 的横坐标为
的横坐标为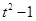 , 2分
, 2分
因为点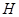 在点
在点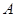 的左侧,所以
的左侧,所以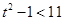 ,即
,即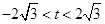 .
.
由已知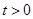 ,所以
,所以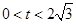 , 4分
, 4分
所以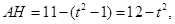
所以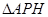 的面积为
的面积为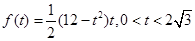 . 6分
. 6分
(Ⅱ)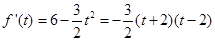 7分
7分
由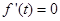 ,得
,得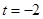 (舍),或
(舍),或 . 8分
. 8分
函数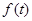 与
与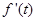 在定义域上的情况如下:
在定义域上的情况如下:
12分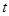
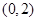
2 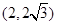
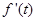
+ 0 
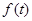
↗ 极大值 ↘
所以当 时,函数
时,函数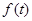 取得最大值8. 13分
取得最大值8. 13分
考点:三角形面积,应用导数研究函数的最值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

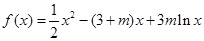 ,
,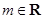 .
. 的单调递增区间;
的单调递增区间;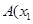 ,
, ,
,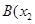 ,
,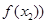 为函数
为函数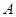 ,
,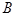 两点的直线
两点的直线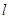 的斜率恒大于
的斜率恒大于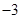 ,求
,求 的取值范围.
的取值范围.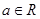 ,函数
,函数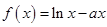 .
.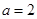 ,求曲线
,求曲线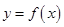 在点
在点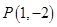 处的切线方程;
处的切线方程; 无零点,求实数
无零点,求实数 的取值范围;
的取值范围; 、
、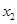 ,求证:
,求证: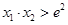 .
.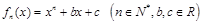
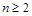 ,
, ,
,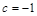 ,证明:
,证明: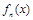 在区间
在区间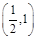 内存在唯一的零点;
内存在唯一的零点;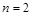 ,若对任意
,若对任意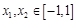 ,均有
,均有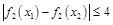 ,求
,求 的取值范围.
的取值范围.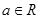 ,函数
,函数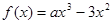 .
.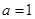 ,求函数
,求函数 的极值与单调区间;
的极值与单调区间;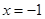 处的切线与直线
处的切线与直线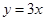 平行,求
平行,求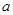 的值;
的值;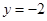 有三个公共点,求
有三个公共点,求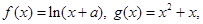 若函数
若函数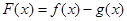 在x = 0处取得极值.
在x = 0处取得极值.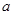 的值;
的值;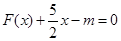 在区间[0,2]上恰有两个不同的实数根,求实数
在区间[0,2]上恰有两个不同的实数根,求实数 的取值范围;
的取值范围; 都成立.
都成立. .
.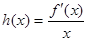 为奇函数,求a的值;
为奇函数,求a的值; 在
在 处取得极大值,求实数a的值;
处取得极大值,求实数a的值;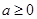 ,求
,求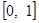 上的最大值.
上的最大值.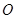 为圆心,
为圆心,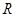 (
(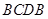 区域(阴影部分)用于种植学校观赏植物,
区域(阴影部分)用于种植学校观赏植物,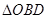 区域用于种植花卉出售,其余区域用于种植草皮出售.已知种植学校观赏植物的成本是每平方米20元,种植花卉的利润是每平方米80元,种植草皮的利润是每平方米30元.
区域用于种植花卉出售,其余区域用于种植草皮出售.已知种植学校观赏植物的成本是每平方米20元,种植花卉的利润是每平方米80元,种植草皮的利润是每平方米30元.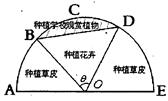
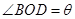 (单位:弧度),用
(单位:弧度),用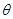 表示弓形
表示弓形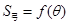 ;
;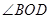 的大小才能使总利润最大?并求出该最大值.
的大小才能使总利润最大?并求出该最大值.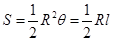 ,
,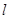 表示扇形的弧长)
表示扇形的弧长)