题目内容
下列命题中正确的序号为
①y=
sin2x的周期为π,最大值为
②若x是第一象限的角,则y=sinx是增函数
③在△ABC中若sinA=sinB则A=B
④α,β∈(0,
)且cosα<sinβ则α+β>
.
①③④
①③④
(你认为正确的都写出来)①y=
| 1 |
| 2 |
| 1 |
| 2 |
②若x是第一象限的角,则y=sinx是增函数
③在△ABC中若sinA=sinB则A=B
④α,β∈(0,
| π |
| 2 |
| π |
| 2 |
分析:①利用三角函数的性质判断.②利用y=sinx的图象和性质判断.③利用诱导公式去判断.④利用y=sinx的性质以及诱导公式判断.
解答:解:①三角函数的周期为T=
=
=π,当sin2x=1时,函数y=
sin2x的最大值为
,所以①正确.
②根据y=sinx的图象可知,函数在第一象限的内不是单调函数,所以②错误.
③在三角形中,若sinA=sinB则A=B或者A=π-B,当A=π-B,时得到A+B=π,显然不成立,舍去,所以必有A=B,所以③正确.
④由题意知cosα<sinβ,即sin(
-α)<sinβ,所以
-α<β,即α+β>
,所以④正确.
故答案为:①③④.
| 2π |
| ω |
| 2π |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②根据y=sinx的图象可知,函数在第一象限的内不是单调函数,所以②错误.
③在三角形中,若sinA=sinB则A=B或者A=π-B,当A=π-B,时得到A+B=π,显然不成立,舍去,所以必有A=B,所以③正确.
④由题意知cosα<sinβ,即sin(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
故答案为:①③④.
点评:本题主要考查了三角函数的图象和性质以及诱导公式,要求熟练掌握相关的运算公式.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
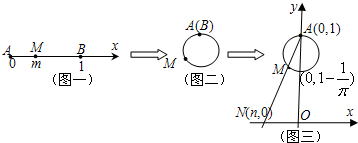 如图揭示了一个由区间(0,1)到实数集R上的对应过程:区间(0,1)内的任意实数m与数轴上的线段AB(不包括端点)上的点M一一对应(图一),将线段AB围成一个圆,使两端A,B恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1)(图三).图三中直线AM与x轴交于点N(n,0),由此得到一个函数n=f(m),则下列命题中正确的序号是( )
如图揭示了一个由区间(0,1)到实数集R上的对应过程:区间(0,1)内的任意实数m与数轴上的线段AB(不包括端点)上的点M一一对应(图一),将线段AB围成一个圆,使两端A,B恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1)(图三).图三中直线AM与x轴交于点N(n,0),由此得到一个函数n=f(m),则下列命题中正确的序号是( )(1)f(
| 1 |
| 2 |
(2)f(x)是偶函数;
(3)f(x)在其定义域上是增函数;
(4)y=f(x)的图象关于点(
| 1 |
| 2 |
| A、(1)(3)(4) |
| B、(1)(2)(3) |
| C、(1)(2)(4) |
| D、(1)(2)(3)(4) |