题目内容
下列命题中正确的序号为
①y=sinxcosx的周期为π,最大值为
; ②若x是第一象限的角,则y=sinx是增函数;③在△ABC中若sinA=sinB则A=B; ④α,β∈(0,
)且cosα<sinβ则α+β>
⑤f(x)=sinx+cosx既不是奇函数,也不是偶函数.
①③④⑤
①③④⑤
(你认为正确的都写出来)学①y=sinxcosx的周期为π,最大值为
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
分析:利用二倍角公式化简①,即可判断①的正误;
直接利用正弦函数的定义判断②的正误;
利用三角方程求出A与B判断③的正误;
利用正弦函数的单调性判断④的正误;
利用两角和的正弦函数,化简函数的表达式,然后判断⑤的正误;
直接利用正弦函数的定义判断②的正误;
利用三角方程求出A与B判断③的正误;
利用正弦函数的单调性判断④的正误;
利用两角和的正弦函数,化简函数的表达式,然后判断⑤的正误;
解答:解:①y=sinxcosx=
sin2x,函数的周期为π,最大值为
;所以①正确;
②若x是第一象限的角,则y=sinx是增函数;显然不正确,
因为函数在[2kπ,2kπ+
]k∈Z,是单调增函数,所以②不正确;
③在△ABC中若sinA=sinB,A、B∈(0,π),则A=B;正确;
④α,β∈(0,
)且cosα<sinβ则cosα=sin(
-α)<sinβ,
所以β>
-α,所以α+β>
正确.
⑤f(x)=sinx+cosx=
sin(x+
),所以函数既不是奇函数,也不是偶函数.正确.
故答案为:①③④⑤.
| 1 |
| 2 |
| 1 |
| 2 |
②若x是第一象限的角,则y=sinx是增函数;显然不正确,
因为函数在[2kπ,2kπ+
| π |
| 2 |
③在△ABC中若sinA=sinB,A、B∈(0,π),则A=B;正确;
④α,β∈(0,
| π |
| 2 |
| π |
| 2 |
所以β>
| π |
| 2 |
| π |
| 2 |
⑤f(x)=sinx+cosx=
| 2 |
| π |
| 4 |
故答案为:①③④⑤.
点评:本题考查三角函数的基本性质,重点是学生对周期性、单调性、奇偶性等知识灵活应用.

练习册系列答案
相关题目
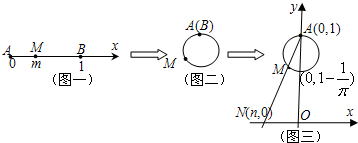 如图揭示了一个由区间(0,1)到实数集R上的对应过程:区间(0,1)内的任意实数m与数轴上的线段AB(不包括端点)上的点M一一对应(图一),将线段AB围成一个圆,使两端A,B恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1)(图三).图三中直线AM与x轴交于点N(n,0),由此得到一个函数n=f(m),则下列命题中正确的序号是( )
如图揭示了一个由区间(0,1)到实数集R上的对应过程:区间(0,1)内的任意实数m与数轴上的线段AB(不包括端点)上的点M一一对应(图一),将线段AB围成一个圆,使两端A,B恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1)(图三).图三中直线AM与x轴交于点N(n,0),由此得到一个函数n=f(m),则下列命题中正确的序号是( )(1)f(
| 1 |
| 2 |
(2)f(x)是偶函数;
(3)f(x)在其定义域上是增函数;
(4)y=f(x)的图象关于点(
| 1 |
| 2 |
| A、(1)(3)(4) |
| B、(1)(2)(3) |
| C、(1)(2)(4) |
| D、(1)(2)(3)(4) |