题目内容

下列命题中正确的序号为
③
③

①一个命题的逆否命题为真，则它的逆命题为假；
②若p：?x∈R，x2+2x+2≤0，则￢p：?x∈R，x2+2x+2＞0；
③设命题p、q，若q是?p的必要不充分条件，则p是￢q的充分不必要条件．
分析：①根据四种命题的关系判断
②根据全称命题的否定判断
③根据四种命题的关系判断
解答：解：①一个命题的逆否命题为真，原命题为真，但逆命题与原命题真假性无关，①错
②若p：?x∈R，x2+2x+2≤0，则￢p：?x∈R，x2+2x+2＞0； 正确
③若q是?p的必要不充分条件，即?p?q，其逆否命题为￢q?p，p应是￢q的必要不充分条件．
综上所述，正确的序号为③
故答案为：③
点评：本题考查四种命题的关系，充要条件的确定．
练习册系列答案
相关题目
4、已知m，n为两条不同的直线，α、β为两个不同的平面，
则下列命题中正确的序号
（4）

（1）m?α，n?α，m∥β，n∥β?α∥β（2） α∥β，m?α，n?β?m∥n（3）m⊥α，m⊥n?n∥α（4）m∥n，n⊥α?m⊥α
符号[x]表示不超过x的最大整数，如[π]=3，[-1.08]=-2，定义函数{x}=x-[x]，那么下列命题中正确的序号是
（2）、（3）
（2）、（3）
．
（1）函数{x}的定义域为R，值域为[0，1]；   
（2）方程{x}=
12
，有无数解；
（3）函数{x}是非奇非偶函数；             
（4）函数{x}是增函数．
下列命题中正确的序号为
①③④⑤
①③④⑤
（你认为正确的都写出来）学
①y=sinxcosx的周期为π，最大值为
1
2
； ②若x是第一象限的角，则y=sinx是增函数；③在△ABC中若sinA=sinB则A=B；   ④α，β∈(0，
π
2
)且cosα＜sinβ则α+β＞
π
2
 ⑤f（x）=sinx+cosx既不是奇函数，也不是偶函数．
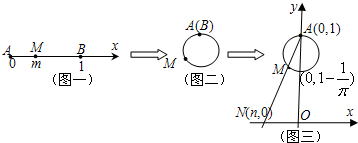精英家教网如图揭示了一个由区间（0，1）到实数集R上的对应过程：区间（0，1）内的任意实数m与数轴上的线段AB（不包括端点）上的点M一一对应（图一），将线段AB围成一个圆，使两端A，B恰好重合（图二），再将这个圆放在平面直角坐标系中，使其圆心在y轴上，点A的坐标为（0，1）（图三）．图三中直线AM与x轴交于点N（n，0），由此得到一个函数n=f（m），则下列命题中正确的序号是（　　）
（1）f（
1
2
）=0；     
（2）f（x）是偶函数；   
（3）f（x）在其定义域上是增函数；
（4）y=f（x）的图象关于点（
1
2
，0）对称．
A、（1）（3）（4）
B、（1）（2）（3）
C、（1）（2）（4）
D、（1）（2）（3）（4）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网