题目内容
已知椭圆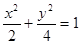
两焦点分别为F1、F2、P是椭圆在第一象限弧上一点，并满足
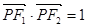，过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点
（1）求P点坐标；
（2）求证直线AB的斜率为定值；
（3）求△PAB面积的最大值。
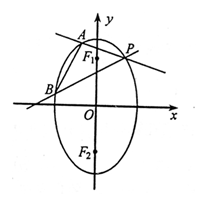
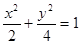两焦点分别为F1、F2、P是椭圆在第一象限弧上一点，并满足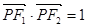，过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点（1）求P点坐标；
（2）求证直线AB的斜率为定值；
（3）求△PAB面积的最大值。
（1）由题可得
则
…………2分
（2）由题意知，两直线PA、PB的斜率必存在，
设PB的斜率为
，…………6分
则BP的直线方程为：
（3）设AB的直线方程：
P到AB的距离为
， …………12分
则
…………2分（2）由题意知，两直线PA、PB的斜率必存在，
设PB的斜率为
，…………6分则BP的直线方程为：
（3）设AB的直线方程：
P到AB的距离为
， …………12分略
练习册系列答案
相关题目
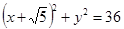及定点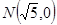
，点P是圆M上的动点，点Q在NP上，点G在MP上，且满足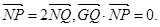
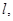与曲线C交于A、B两点，O是坐标原点，设
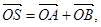是否存在这样的直线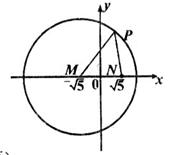
,它的离心率为
.直线
与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程.
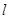与离心率e=
的椭圆C：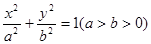
交于P、Q两点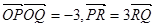，直线
，求直线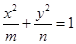
（m＞n＞0）和双曲线
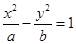（a＞b＞0）有相同的焦点F1，F2，P是两条曲线的一个交点，则|PF1|·|PF2|的值是 （ ）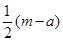
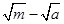
＋y2＝1共焦点且过点P(2,1)的双曲线方程是( )
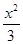－y2＝1
－＝1 
＝1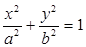
的右焦点，点P在椭圆上，△POF2是面积为
的正三角形，则b2的值是 ▲ 