题目内容
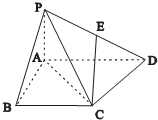 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与平面ABCD所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与平面ABCD所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=| 1 | 2 |
(1)求证:平面PAC⊥面PCD;
(2)在棱PD上找一点E,使CE∥面PAB,并说明理由;
(3)在(2)的前提下,求二面角E-AC-D的大小.
分析:(1)由已知中PA⊥平面ABCD,∠PBA=45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=
AD,由勾股定理可得AC⊥CD,PA⊥CD,再由线面垂直的判定定理可得CD⊥面PAC,再由面面垂直的判定定理即可得到答案.
(2)取棱PD的中点E,做EF⊥AD于F,则F为AD的中点,根据三角形中位线定理可得EF∥PA,根据线面平行的判定定理,我们可得CE∥面PAB;
(3)先过F作FG垂直AC于G,得∠EGF即为二面角E-AC-D的平面角;最后通过求EF以及FG的长即可求出结论.
| 1 |
| 2 |
(2)取棱PD的中点E,做EF⊥AD于F,则F为AD的中点,根据三角形中位线定理可得EF∥PA,根据线面平行的判定定理,我们可得CE∥面PAB;
(3)先过F作FG垂直AC于G,得∠EGF即为二面角E-AC-D的平面角;最后通过求EF以及FG的长即可求出结论.
解答:证明: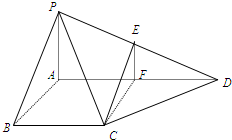 (1)设PA=1,由题意PA=BC=1,AD=2.
(1)设PA=1,由题意PA=BC=1,AD=2.
∵PA⊥面ABCD,∴PA⊥AB,而∠PBA=45°,∴AB=1,
又∠ABC=∠BAD=90°,得CD=AC=
.
由勾股定理逆定理得AC⊥CD.
又∵PA⊥CD,PA∩AC=A,
∴CD⊥面PAC,
又CD?面PCD,∴面PAC⊥面PCD.
(2)取E为PD的中点,作EF⊥AD于F,则F为AD的中点,且EF∥PA,
∴EF∥平面PAB,
由F为AD的中点以及PA=BC=
AD可得AF=BC,AF∥BC
所以;ABCF为平行四边形;
∴CF∥AB;
CF∥平面PAB,
得到平面EFC∥平面PAB,
∴CE∥面PAB
(3)由第二问知,EF⊥平面ABCD;
过F作FG垂直AC于G,
由三垂线定理得∠EGF即为二面角E-AC-D的平面角.
由第一问得到的AC⊥CD
可得FG∥CD,FG=
CD,
在RT△EFG中,EF=
PA=
,FG=
CD=
.
∴tan∠EGF=
=
.
∴二面角E-AC-D的大小为:arctan
.
 (1)设PA=1,由题意PA=BC=1,AD=2.
(1)设PA=1,由题意PA=BC=1,AD=2.∵PA⊥面ABCD,∴PA⊥AB,而∠PBA=45°,∴AB=1,
又∠ABC=∠BAD=90°,得CD=AC=
| 2 |
由勾股定理逆定理得AC⊥CD.
又∵PA⊥CD,PA∩AC=A,
∴CD⊥面PAC,
又CD?面PCD,∴面PAC⊥面PCD.
(2)取E为PD的中点,作EF⊥AD于F,则F为AD的中点,且EF∥PA,
∴EF∥平面PAB,
由F为AD的中点以及PA=BC=
| 1 |
| 2 |
所以;ABCF为平行四边形;
∴CF∥AB;
CF∥平面PAB,
得到平面EFC∥平面PAB,
∴CE∥面PAB
(3)由第二问知,EF⊥平面ABCD;
过F作FG垂直AC于G,
由三垂线定理得∠EGF即为二面角E-AC-D的平面角.
由第一问得到的AC⊥CD
可得FG∥CD,FG=
| 1 |
| 2 |
在RT△EFG中,EF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴tan∠EGF=
| EF |
| FG |
| ||
| 2 |
∴二面角E-AC-D的大小为:arctan
| ||
| 2 |
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面平行的判定,其中(1)的关键是证得CD⊥面PAC,(2)的关键是证得EF∥PA.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=