题目内容
(本小题满分12分)
已知一四棱锥P-ABCD的三视图如下,E是侧棱PC上的动点。

(Ⅰ)求四棱锥P-ABCD的体积;
(Ⅱ)当点E在何位置时,BD⊥AE?证明你的结论;
(Ⅲ)若点E为PC的中点,求二面角D-AE-B的大小.
(Ⅰ) ;(Ⅱ)不论点E在何位置,都有BD⊥AE;(Ⅲ)
;(Ⅱ)不论点E在何位置,都有BD⊥AE;(Ⅲ)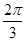 。
。
解析试题分析:(Ⅰ)解:由该四棱锥的三视图可知,该四棱锥P-ABCD的底面是边长为1的正方形,
侧棱PC⊥底面ABCD,且PC="2." 

∴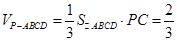 ----------------------------2分
----------------------------2分
(Ⅱ) 不论点E在PC上何位置,都有BD⊥AE---------------------------------------3分
证明如下:连结AC,∵ABCD是正方形
∴BD⊥AC ∵PC⊥底面ABCD 且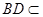 平面
平面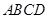 ∴BD⊥PC-----------5分
∴BD⊥PC-----------5分
又∵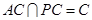 ∴BD⊥平面PAC
∴BD⊥平面PAC
∵不论点E在何位置,都有AE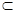 平面PAC
平面PAC
∴不论点E在何位置,都有BD⊥AE ----------------------------------------------7分
(Ⅲ) 解法一:在平面DAE内过点D作DG⊥AE于G,连结BG
∵CD="CB,EC=EC," ∴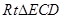 ≌
≌
∴ED="EB," ∵AD=AB ∴△EDA≌△EBA
∴BG⊥EA ∴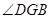 为二面角D-EA-B的平面角--------------------------10分
为二面角D-EA-B的平面角--------------------------10分
∵BC⊥DE, AD∥BC ∴AD⊥DE
在Rt△ADE中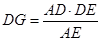 =
=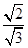 =BG
=BG
在△DGB中,由余弦定理得
∴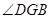 =
=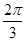 -----------------------12分
-----------------------12分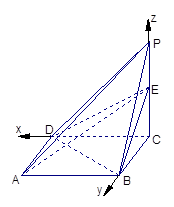
[解法二:以点C为坐标原点,CD所在的直线为x轴建立空间直角坐标系如图示:
则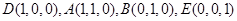 ,从
,从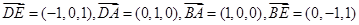
设平面ADE和平面ABE的法向量分别为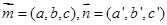
由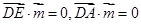 可得:
可得: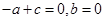 ,
,
同理得: 。令
。令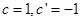 ,则
,则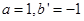 ,
,
∴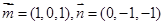 ------10分
------10分
设二面角D-AE-B的平面角为 ,则
,则 ∴
∴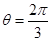 ------12分
------12分
考点:锥体的体积公式;线面垂直的判定定理;线面垂直的性质定理;二面角。
点评:二面角的求法是立体几何中的一个难点。我们解决此类问题常用的方法有两种:①综合法,综合法的一般步骤是:一作二说三求。②向量法,运用向量法求二面角应注意的是计算。很多同学都会应用向量法求二面角,但结果往往求不对,出现的问题就是计算错误。

 全能测控期末小状元系列答案
全能测控期末小状元系列答案
 是双曲线
是双曲线

 上一点,
上一点, 、
、 分别是双曲线
分别是双曲线 的左、右顶点,直线
的左、右顶点,直线 ,
,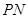 的斜率之积为
的斜率之积为 .
.
 ,
, 两点,
两点, 为坐标原点,
为坐标原点, 为双曲线上一点,满足
为双曲线上一点,满足 ,求
,求 的值.
的值. 中,
中, ,
, ,点
,点 在
在 上,
上, 交
交 于
于 ,
, 交
交 于
于 .沿
.沿 将△
将△ 翻折成△
翻折成△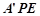 ,使平面
,使平面 平面
平面 将△
将△ 翻折成△
翻折成△ ,使平面
,使平面 平面
平面
 平面
平面 ,当
,当 为何值时,二面角
为何值时,二面角 的大小为
的大小为 ?
?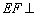 平面AEB,
平面AEB, ,
, ,
,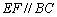 ,
,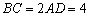 ,
,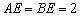 ,
, ,G是BC的中点.
,G是BC的中点.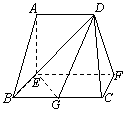
 ;
; 的大小.
的大小.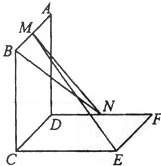
 中,
中, ⊥平面
⊥平面 ,
, 为
为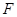 为
为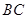 的中点,底面
的中点,底面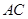 ,
, 交于点
交于点 .
.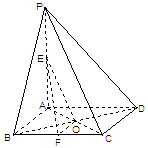
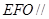 平面
平面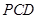 ;
; ⊥平面
⊥平面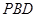 .
.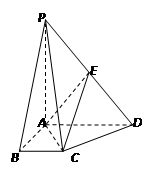
 是正三角形,AB
是正三角形,AB 平面BCD,
平面BCD, ,E为BC的中点,F在棱AC上,且
,E为BC的中点,F在棱AC上,且

 BAD=90°,PA
BAD=90°,PA 底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.