题目内容
如图,在△ 中,
中, ,
, ,点
,点 在
在 上,
上, 交
交 于
于 ,
, 交
交 于
于 .沿
.沿 将△
将△ 翻折成△
翻折成△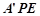 ,使平面
,使平面 平面
平面 ;沿
;沿 将△
将△ 翻折成△
翻折成△ ,使平面
,使平面 平面
平面 .
.
(Ⅰ)求证: 平面
平面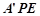 .
.
(Ⅱ)设 ,当
,当 为何值时,二面角
为何值时,二面角 的大小为
的大小为 ?
?
(1)要证明线面平行,则可以根据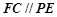 来得到证明。
来得到证明。
(2)
解析试题分析:解:(Ⅰ)因为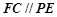 ,
, 平面
平面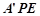 ,所以
,所以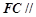 平面
平面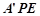 . …2分
. …2分
因为平面 平面
平面 ,且
,且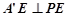 ,所以
,所以 平面
平面 .
.
同理,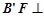 平面
平面 ,所以
,所以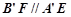 ,从而
,从而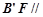 平面
平面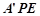 . …4分
. …4分
所以平面 平面
平面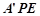 ,从而
,从而 平面
平面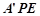 . …6分
. …6分
(Ⅱ)以C为原点,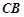 所在直线为
所在直线为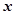 轴,
轴,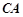 所在直线为
所在直线为 轴,过C且垂直于平面
轴,过C且垂直于平面 的直线为
的直线为 轴,建立空间直角坐标系,如图. …7分
轴,建立空间直角坐标系,如图. …7分
则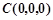 ,
,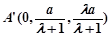 ,
, ,
,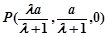 .
.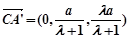 ,
,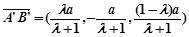 ,
, .
.
平面 的一个法向量
的一个法向量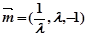 , …9分
, …9分
平面 的一个法向量
的一个法向量 . …11分
. …11分
由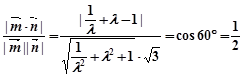 , …13分
, …13分
化简得 ,解得
,解得 . …15分
. …15分
考点:线面平行和二面角的求解
点评:解决的关键是利用空间向量法来得到空间中的二面角的表示,以及结合判定定理得到线面的垂直的证明。属于基础题。

练习册系列答案
相关题目
 ,AB=2CD=8.
,AB=2CD=8.
 的底面
的底面 为一直角梯形,其中
为一直角梯形,其中 ,
,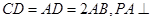 底面
底面 是
是 的中点.
的中点.
 //平面
//平面 ;
; 平面
平面 ,求平面
,求平面 与平面
与平面 夹角的余弦值.
夹角的余弦值. ,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点。
,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点。
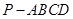 中,
中,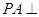 平面ABCD,底面ABCD是菱形,
平面ABCD,底面ABCD是菱形,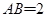 ,
,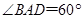 .
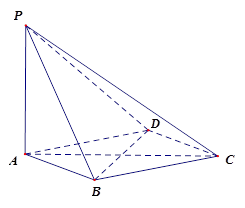
.
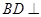 平面PAC;
平面PAC;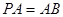 ,求PB与AC所成角的余弦值;
,求PB与AC所成角的余弦值;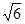 ,求证:平面PBC⊥平面PDC
,求证:平面PBC⊥平面PDC
 平面EFGH;
平面EFGH; 与正三角形
与正三角形 所在的平面相互垂直,且
所在的平面相互垂直,且 、
、
 、
、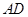 中点.
中点.
 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.

 中,
中,
 ,
,  ,D为AB中点。
,D为AB中点。
 ;
; ∥平面
∥平面 ;
;