题目内容

 是双曲线
是双曲线

 上一点,
上一点, 、
、 分别是双曲线
分别是双曲线 的左、右顶点,直线
的左、右顶点,直线 ,
,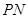 的斜率之积为
的斜率之积为 .
.
(1)求双曲线的离心率;
(2)过双曲线 的右焦点且斜率为1的直线交双曲线于
的右焦点且斜率为1的直线交双曲线于 ,
, 两点,
两点, 为坐标原点,
为坐标原点, 为双曲线上一点,满足
为双曲线上一点,满足 ,求
,求 的值.
的值.
(1) e=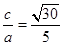 . (2)λ=0或λ=-4.
. (2)λ=0或λ=-4.
解析试题分析:(1)点P(x0,y0)(x0≠±a)在双曲线 =1上,有
=1上,有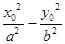 =1, 1分
=1, 1分
由题意又有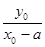 ·
·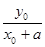 =
= , 2分
, 2分
可得a2=5b2,c2=a2+b2=6b2,则e=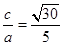 . 4分
. 4分
(2)联立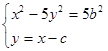 ,得4x2-10cx+35b2=0,设A(x1,y1),B(x2,y2)
,得4x2-10cx+35b2=0,设A(x1,y1),B(x2,y2)
则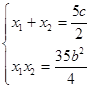 ① 6分
① 6分
设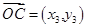 ,
, ,即
,即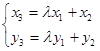
又C为双曲线上一点,即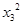 -5
-5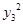 =5b2,有(λx1+x2)2-5(λy1+y2)2=5b2 。7分
=5b2,有(λx1+x2)2-5(λy1+y2)2=5b2 。7分
化简得:λ2(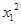 -5
-5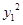 )+(
)+( -5
-5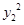 )+2λ(x1x2-5y1y2)=5b2 。9分
)+2λ(x1x2-5y1y2)=5b2 。9分
又A(x1,y1),B(x2,y2)在双曲线上,所以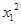 -5
-5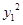 =5b2,
=5b2, -5
-5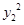 =5b2
=5b2
由①式又有x1x2-5y1y2=x1x2-5(x1-c)(x2-c)=-4x1x2+5c(x1+x2)-5c2=10b2
得λ2+4λ=0,解出λ=0或λ=-4. 12分
考点:本题主要考查双曲线标准方程及其几何性质,直线与双曲线的位置关系,平面向量的线性运算。
点评:难题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题利用双曲线的标准方程,确定得到离心率。本题(II)在利用韦达定理的基础上,又利于点在曲线上得到λ的方程,使问题得解。

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
 中,底面
中,底面 为正三角形,
为正三角形,
 平面ABC,
平面ABC, 的中点,M是线段
的中点,M是线段 上的动点。
上的动点。
 ,请给出证明;
,请给出证明;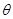 ,求
,求 的最大值。
的最大值。 ,AB=2CD=8.
,AB=2CD=8.

 , 若存在, 求CE的长, 若不存在,
, 若存在, 求CE的长, 若不存在,  ,
, ∥
∥ ,
, .又
.又 ,
, ,直线AM与直线PC所成的角为
,直线AM与直线PC所成的角为 .
.
 ;
; 的余弦值.
的余弦值.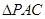 与
与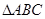 是均以
是均以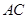 为斜边的等腰直角三角形,
为斜边的等腰直角三角形, ,
,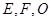 分别为
分别为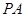 ,
,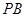 ,
,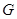 为
为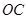 的中点,且
的中点,且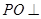 平面
平面 .
.
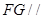 平面
平面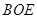 ;
;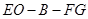 的余弦值.
的余弦值. 的底面
的底面 为一直角梯形,其中
为一直角梯形,其中 ,
,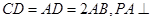 底面
底面 是
是 的中点.
的中点.
 //平面
//平面 ;
; 平面
平面 ,求平面
,求平面 与平面
与平面 夹角的余弦值.
夹角的余弦值. ,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点。
,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点。

