题目内容
(本小题满分12分)如图,四棱锥P-ABCD的底面ABCD是直角梯形,∠DAB=∠ABC=90o,PA⊥底面ABCD,PA=AB=AD=2,BC=1,E为PD的中点.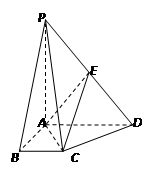
(1) 求证:CE∥平面PAB;
(2) 求PA与平面ACE所成角的大小;
(3) 求二面角E-AC-D的大小.
(1) 取PA的中点F,连结FE、FB,则FE∥BC,且FE=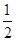 AD=BC,∴BCEF是平行四边形,∴CE∥BF,而BFÌ平面PAB,∴CE∥平面PAB.(2) arcsin
AD=BC,∴BCEF是平行四边形,∴CE∥BF,而BFÌ平面PAB,∴CE∥平面PAB.(2) arcsin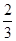 (3) arccos
(3) arccos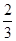
解析试题分析:(1)证明:取PA的中点F,连结FE、FB,则
FE∥BC,且FE=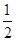 AD=BC,∴BCEF是平行四边形,
AD=BC,∴BCEF是平行四边形,
∴CE∥BF,而BFÌ平面PAB,∴CE∥平面PAB.
(2) 解:取 AD的中点G,连结EG,则EG∥AP,问题转为求EG与平面ACE所成角的大小.又设点G到平面ACE的距离为GH,H为垂足,连结EH,则∠GEH为直线EG与平面ACE所成的角.现用等体积法来求GH.
∵VE-AGC=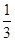 S△AGC·EG=
S△AGC·EG=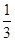
又AE=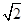 ,AC=CE=
,AC=CE=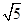 ,易求得S△AEC=
,易求得S△AEC=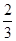 ,
,
∴VG-AEC=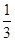 ´
´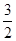 ´GH=VE-AGC=
´GH=VE-AGC=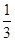 ,∴GH=
,∴GH=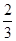
在Rt△EHG中,sin∠GEH=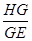 =
=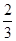 ,即PA与平面ACE所成的角为arcsin
,即PA与平面ACE所成的角为arcsin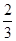 .
.
(3) 设二面角E-AC-D的大小为a.
由面积射影定理得cosa=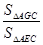 =
=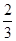 ,∴a=arccos
,∴a=arccos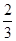 ,即二面角E-AC-D的大小为arccos
,即二面角E-AC-D的大小为arccos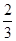 .
.
考点:线面平行的判定及线面角二面角的求解
点评:本题还可利用空间向量求解,利用AB,AD,AP两两垂直,以A为原点建立坐标系,根据线段长度写出各点坐标,带入相应的公式计算求角

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 的底面
的底面 为一直角梯形,其中
为一直角梯形,其中 ,
,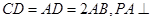 底面
底面 是
是 的中点.
的中点.
 //平面
//平面 ;
; 平面
平面 ,求平面
,求平面 与平面
与平面 夹角的余弦值.
夹角的余弦值. 与正三角形
与正三角形 所在的平面相互垂直,且
所在的平面相互垂直,且 、
、
 、
、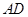 中点.
中点.
 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.


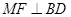 ;
;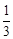 ,求AB的长.
,求AB的长. ⊥平面
⊥平面 ,
,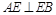 ,
,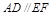 ,
,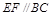 ,
,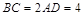 ,
,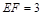 ,
,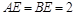 ,
,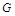 是
是 的中点.
的中点.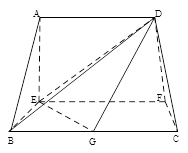
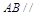 平面
平面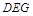 ;
;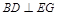 ;
;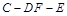 的余弦值.
的余弦值.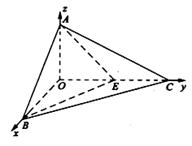
 中,
中,
 ,
,  ,D为AB中点。
,D为AB中点。
 ;
; ∥平面
∥平面 ;
;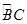 的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图).
的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图).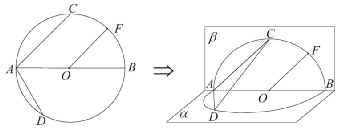
 上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求直线AG与平面ACD所成角的正弦值;若不存在,请说明理由.
上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求直线AG与平面ACD所成角的正弦值;若不存在,请说明理由.