题目内容

已知在平面直角坐标系xOy中，O（0，0），A（1，2），B（1，1），C（2，-1），动点M（x，y）满足条件 
-2≤
OM
?
OA
≤2
1≤
OM
?
OB
≤2
  则
OM
?
OC
的最大值为（　　）
A、16B、8C、12D、15
分析：利用向量的数量积的坐标表示把已知转化可得
-2≤x+2y≤2
1≤x+y≤2
，作出对应的平面区域，z=
OM
•
OC
=2x-y，利用 线性规划的知识即可求
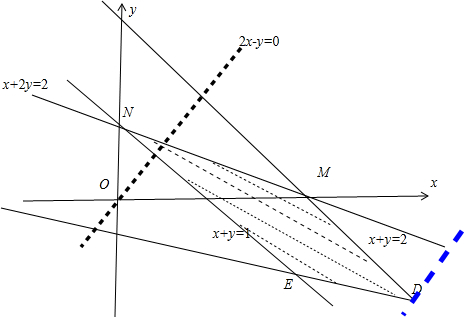解答：精英家教网解：∵O（0，0），A（1，2），B（1，1），C（2，-1），M（x，y）
∴
OA
=(1，2)，
OB
=(1，1)，
OC
=（2，-1）
∴
OM
•
OA
=x+2y，
OM
•
OB
=x+y
∴
-2≤x+2y≤2
1≤x+y≤2
，其对应的平面区域如图所示的阴影部分
令z=
OM
•
OC
=2x-y
则y=2x-z，-z表示直线y=2x-z在y轴截距的相反数，截距越小，z越大
结合图形可知，当z=2x-y经过点D时，z最大
由
x+2y=-2
x+y=2
可得D（6，-4），此时z=16
故最大值为：16
点评：本题主要考查了以向量的 数量积的坐标表示为载体，求解目标函数在可行域下的最优解，属于知识的简单应用
练习册系列答案
相关题目
选修4-4：坐标系与参数方程
已知在平面直角坐标系xOy内，点P（x，y）在曲线C：
x=1+cosθ
y=sinθ
(θ为参数，θ∈R）上运动．以Ox为极轴建立极坐标系，直线l的极坐标方程为ρcos(θ+
π
4
)=0．
（Ⅰ）写出曲线C的标准方程和直线l的直角坐标方程；
（Ⅱ）若直线l与曲线C相交于A、B两点，点M在曲线C上移动，试求△ABM面积的最大值，并求此时M点的坐标．
已知在平面直角坐标系中的一个椭圆，它的中心在原点，左焦点为F(-
3
，0)，且过点D（2，0）．
（1）求该椭圆的标准方程；
（2）设点A(1，
1
2
)，若P是椭圆上的动点，求线段PA的中点M的轨迹方程．
（坐标系与参数方程选做题）已知在平面直角坐标系xoy中，圆C的参数方程为
x=
3
+3cosθ
y=1+3sinθ
，（θ为参数），以ox为极轴建立极坐标系，直线l的极坐标方程为ρcos(θ+
π
6
)=0，则圆C截直线l所得的弦长为
4
2
4
2
．
已知在平面直角坐标系中，O（0，0），A（1，-2），B（1，1），C（2，-1），动点M（x，y）满足条件
-2≤
OM
•
OA
≤2
1≤
OM
•
OB
≤2
，则z=
OM
•
OC
的最大值为（　　）
A、-1B、0C、3D、4
已知在平面直角坐标系xOy中的一个椭圆，它的中心在原点，左焦点为F(-
3
，0)，右顶点为D（2，0），设点A(1，
1
2
)．
（Ⅰ）求该椭圆的标准方程；
（Ⅱ）若P是椭圆上的动点，求线段PA中点M的轨迹方程；
（Ⅲ）是否存在直线l，满足l过原点O并且交椭圆于点B、C，使得△ABC面积为1？如果存在，写出l的方程；如果不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网