题目内容
(坐标系与参数方程选做题)已知在平面直角坐标系xoy中,圆C的参数方程为
,(θ为参数),以ox为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ+
)=0,则圆C截直线l所得的弦长为
|
| π |
| 6 |
4
| 2 |
4
.| 2 |
分析:首先把给出的圆的参数方程和直线的极坐标方程化为普通方程,然后运用数形结合即可解得答案.
解答: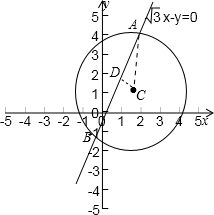 解:由
解:由
,得
,两式平方相加得:(x-
)2+(y-1)2=9 ①,
由ρcos(θ+
)=0,得:ρ(cosθcos
-sinθsin
)=0,即
x-y=0 ②,
如图
圆心C(
,1)到直线
x-y=0的距离为
=1,
所以直线L被圆C所截得的弦长为|AB|=2
=4
.
故答案为4
.
 解:由
解:由
|
|
| 3 |
由ρcos(θ+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 3 |
如图
圆心C(
| 3 |
| 3 |
|
| ||||
|
所以直线L被圆C所截得的弦长为|AB|=2
| 32-12 |
| 2 |
故答案为4
| 2 |
点评:本题考查了简单曲线的极坐标方程和圆的参数方程,考查了数形结合的解题思想,考查了灵活处理和解决问题的能力,是中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目