题目内容
已知等比数列{an} 的前n项和为Sn,若S4=1,S8=4,则a13+a14+a15+a16=( )A.7
B.16
C.27
D.64
【答案】分析:由给出的数列{an}是等比数列,则该数列的第一个四项和、第二个四项和、…仍然构成等比数列,利用等比数列的通项公式求a13+a14+a15+a16的值.
解答:解:因为数列{an}是等比数列,所以,该数列的第一个四项和,第二个四项和,第三个四项和,第四个四项和依然构成等比数列,则其公比q=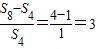 ,
,
所以,a13+a14+a15+a16= .
.
故选C.
点评:本题考查了等比数列的性质,如果一个数列是等比数列,则该数列的第一个n项和,第二个n项和,…依然构成等比数列,且公比为原等比数列公比的n次方,此题是中档题.
解答:解:因为数列{an}是等比数列,所以,该数列的第一个四项和,第二个四项和,第三个四项和,第四个四项和依然构成等比数列,则其公比q=
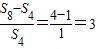 ,
,所以,a13+a14+a15+a16=
 .
.故选C.
点评:本题考查了等比数列的性质,如果一个数列是等比数列,则该数列的第一个n项和,第二个n项和,…依然构成等比数列,且公比为原等比数列公比的n次方,此题是中档题.

练习册系列答案
相关题目