题目内容
(本小题满分13分)
已知 ,
,  是平面上一动点,
是平面上一动点,  到直线
到直线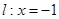 上的射影为点
上的射影为点 ,且满足
,且满足
(Ⅰ)求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过点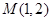 作曲线
作曲线 的两条弦
的两条弦 , 设
, 设 所在直线的斜率分别为
所在直线的斜率分别为 , 当
, 当 变化且满足
变化且满足 时,证明直线
时,证明直线 恒过定点,并求出该定点坐标.
恒过定点,并求出该定点坐标.
(1) y2="4x" (2) 直线AB经过(5,-6)这个定点
解析试题分析:解: (Ⅰ)设曲线C上任意一点P(x,y), 又F(1,0),N(-1,y),从而
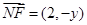 ,
, ,
,
化简得y2="4x," 即为所求的P点的轨迹C的对应的方程. ………………4分
(Ⅱ)设 、
、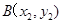 、
、 、
、
将MB与 联立,得:
联立,得:
∴ ①
①
同理  ②
②
而AB直线方程为:  ,即
,即 ③
③
………………8分
由①②:y1+y2=
代入③,整理得 恒成立………………10分
恒成立………………10分
则 故直线AB经过(5,-6)这个定点.. ………………13分
故直线AB经过(5,-6)这个定点.. ………………13分
考点:轨迹方程,直线与抛物线的位置关系
点评:解决该试题的关键是利用设点,得到关系式,然后坐标化,进而化简得到轨迹方程。属于基础题。

练习册系列答案
相关题目
设向量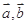 满足:
满足: ,则向量
,则向量 与
与 的夹角为( ).
的夹角为( ).
A. | B.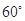 | C. | D. |
 的三个内角A,B,C所对的边分别为a,b,c, 向量
的三个内角A,B,C所对的边分别为a,b,c, 向量
 且
且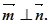
 的大小;
的大小; ②
② ③
③ ④
④ .试从中再选择两个条件以确定
.试从中再选择两个条件以确定 的面积.
的面积. =
= ,
, =
= ,
, 为锐角.
为锐角. ,求sin
,求sin 中,点
中,点 在线段
在线段 上,且
上,且 ,延长
,延长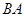 到
到 ,使
,使 .设
.设 .
.
 表示向量
表示向量 ;
;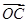 与
与 共线,求
共线,求 的值.
的值.  |=1,|
|=1,| |=
|= ;(I)若
;(I)若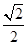 ,求
,求 与
与 的夹角;(II)若
的夹角;(II)若 ,求|
,求| =
=  ,
, =(1,2)
=(1,2) 的值。
的值。
 ,
, ,求
,求 ,
, .
. 和
和 ;
; 为何值时,
为何值时, .
. ,
,
 的最小正周期;
的最小正周期; ,求函数
,求函数