题目内容
设向量 =
= ,
, =
= ,
, 为锐角.
为锐角.
(1)若 ∥
∥ ,求tanθ的值;
,求tanθ的值;
(2)若 ·
· =
= ,求sin
,求sin +cos
+cos 的值.
的值.
(1)2(2)
解析试题分析:(1)∵ =
= ,
, =
= ,且
,且 ∥
∥ 2分
2分
∴ 2 cos - sin
- sin =0,∴tanθ=2. 5分
=0,∴tanθ=2. 5分
(2)因为a·b=2+sinθcosθ= ,所以sinθcosθ=
,所以sinθcosθ= . 8分
. 8分
所以 (sinθ+cosθ)2=1+2 sinθcosθ= . 10分
. 10分
又因为θ为锐角,所以sinθ+cosθ= . 12分
. 12分
考点:向量的数量积,同角关系式
点评:解决的关键是利用向量的共线来得到正切值,然后结合同角关系式来求解,属于基础题。

练习册系列答案
相关题目
已知 ,
, ,若
,若 为满足
为满足 的一随机整数,则
的一随机整数,则 是直角三角形的概率为( )
是直角三角形的概率为( )
A. | B. | C. | D. |
 =(cosα,sinα),
=(cosα,sinα), =(cosβ,sinβ),
=(cosβ,sinβ), |
| ;
; ,
, 。
。 ,
, ;(2)若
;(2)若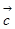 为单位向量,求
为单位向量,求
 的值;
的值;  ,且
,且 ,求
,求 的值.
的值. ,
, ,函数
,函数
 的解析式及其单调递增区间;
的解析式及其单调递增区间; 中,角
中,角 为钝角,若
为钝角,若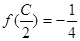 ,
, ,
, .求
.求 ,且x∈[0,
,且x∈[0, ],求
],求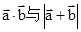 ;
; 的最小值是
的最小值是 ,求实数
,求实数 的值。
的值。 与
与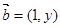 共线,且有函数
共线,且有函数
 ,边
,边 ,
, ,求AC的长.
,求AC的长.  ,
,  是平面上一动点,
是平面上一动点, 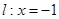 上的射影为点
上的射影为点 ,且满足
,且满足
 的方程;
的方程;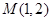 作曲线
作曲线 , 设
, 设 , 当
, 当 时,证明直线
时,证明直线 恒过定点,并求出该定点坐标.
恒过定点,并求出该定点坐标.