题目内容
定义在(-1,1)上的函数f(x)满足:对任意x,y∈(-1,1),f(x)-f(y)=f(
)恒成立.有下列结论:①f(0)=0;②函数f(x)为(-1,1)上的奇函数;③函数f(x)是定义域内的增函数;④若an+1=
(n∈N*),且an∈(-1,0)∪(0,1),则数列{f(an)}为等比数列.
其中你认为正确的所有结论的序号是
| x-y |
| 1-xy |
| 2an | ||
1+
|
其中你认为正确的所有结论的序号是
①②④
①②④
.分析:①取x=y=0代入已知的等式,则可求f(0)=0;
②取x=0,y=x,代入已知等式,整理后可得函数f(x)为奇函数;
③取x,y∈(-1,1),可证出-1<
<0,当f(
)>0时,不能证明函数f(x)是定义域内的增函数;
④运用奇函数定义,得f(an)+f(an)=f(an)-f(-an)=f(
)=f(an+1),整理后可得数列{f(an)}为等比数列.
②取x=0,y=x,代入已知等式,整理后可得函数f(x)为奇函数;
③取x,y∈(-1,1),可证出-1<
| x-y |
| 1-xy |
| x-y |
| 1-xy |
④运用奇函数定义,得f(an)+f(an)=f(an)-f(-an)=f(
| 2an |
| 1+an2 |
解答:解:①由对任意x,y∈(-1,1),f(x)-f(y)=f(
)恒成立.
取x=y=0,则f(0)-f(0)=f(
)=f(0),所以f(0)=0,所以①正确;
②取x=0,y=x,则f(0)-f(x)=f(
)=f(-x),即f(-x)=-f(x),
所以函数f(x)为(-1,1)上的奇函数,所以②正确;
③设-1<x<y<1,则-2<x<0,xy<1,1-xy>0,所以
<0,
又
+1=
=
>0,
所以-1<
<0,
若f(
)>0,则f(x)-f(y)=f(
)>0,有f(x)>f(y),此时函数为减函数,
所以③不正确;
④由f(an)+f(an)=f(an)-f(-an)=f(
)=f(an+1),所以f(an+1)=2f(an),
又an∈(-1,0)∪(0,1),所以f(an)≠0,所以数列{f(an)}为等比数列.
所以④正确.
故答案为①②④.
| x-y |
| 1-xy |
取x=y=0,则f(0)-f(0)=f(
| 0-0 |
| 1-0 |
②取x=0,y=x,则f(0)-f(x)=f(
| 0-x |
| 1-0•x |
所以函数f(x)为(-1,1)上的奇函数,所以②正确;
③设-1<x<y<1,则-2<x<0,xy<1,1-xy>0,所以
| x-y |
| 1-xy |
又
| x-y |
| 1-xy |
| x-y+1-xy |
| 1-xy |
| (1-y)(1+x) |
| 1-xy |
所以-1<
| x-y |
| 1-xy |
若f(
| x-y |
| 1-xy |
| x-y |
| 1-xy |
所以③不正确;
④由f(an)+f(an)=f(an)-f(-an)=f(
| 2an |
| 1+an2 |
又an∈(-1,0)∪(0,1),所以f(an)≠0,所以数列{f(an)}为等比数列.
所以④正确.
故答案为①②④.
点评:本题考查了命题的真假判断与应用,考查了特值思想,解答此题的关键是把x,y取特值后灵活变形,考查了学生的观察能力和灵活解决问题的能力,此题是中档题.

练习册系列答案
相关题目
 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.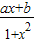 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.