Question

【题目】设函数由方程确定，对于函数给出下列命题：

①存在，，使得成立；

②，，使得且同时成立；

③对于任意，恒成立；

④对任意，，；都有恒成立．

其中正确的命题共有（ ）

A.1个B.2个C.3个D.4个

Answer 1

【答案】A

【解析】

将方程的绝对值符号去掉，画出函数的图象，对命题逐一判断，得:

对①，函数在上递减，故①错误；

对②，即，均在图象上，讨论点分别在第一、二、四象限代入方程，看是否有实数解；

对③，恒成立，即恒成立，由图的图象总在图象的上方，故③正确；

对④，可通过举出反例确定④错误.

由方程知，

当且时，方程为；

当且时，方程为，不成立；

当且时，方程为；

当且时，方程为，不成立；

作出函数的图象如图所示，

对于①，是定义域R上的单调减函数，

则对任意，都有恒成立，①错误；

对于②，假设点在第一象限，则点也在第一象限，

所以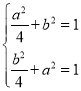，该方程组没有实数解，所以该情况不可能；

假设点在第四象限，则点在第二象限，

所以，该方程组没有实数解，所以该种情况不可能；

同理点在第二象限，则点在第四象限，也不可能．

故该命题是假命题．

对于③，由图形知，对于任意，有

即恒成立，③正确；

对于④，不妨令，

则为，

又由题，则 ，

即不恒成立，所以④错误．

综上知，正确的命题序号是③．

故选：A