题目内容

（2010•青浦区二模）一个用立方块搭成的立体图形，小张从前面看和从上面看到的图形都是同一图形，如图，那么，搭成这样一个立体图形最少需要
5
5
个小立方块．
分析：画出几何体的图形如图，可求搭成这样一个立体图形最少需要的小立方块的数目．
解答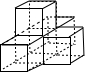：解：有题意画出图形，
即可求出最少需要的小立方块的数目是5．
故答案为：5
点评：本题考查简单几何体的三视图，是基础题．
练习册系列答案
相关题目
（2010•青浦区二模）以抛物线y2=8x的顶点为中心，焦点为右焦点，且以y=±
3
x为渐近线的双曲线方程是
x2-
y2
3
=1
x2-
y2
3
=1
．
（2010•青浦区二模）函数y=sinxcosx+
3
的最小正周期为
π
π
．
（2010•青浦区二模）[文科]非负实数x、y满足
2x+y-4≤0
x+y-3≤0
，则x+3y的最大值为
9
9
．
（2010•青浦区二模）[理科]观察下列式子：1+
1
22
＜
3
2
，1+
1
22
+
1
32
＜
5
3
，1+
1
22
+
1
32
+
1
42
＜
7
4
，…，可以猜想结论为（　　）
（2010•青浦区二模）[理科]定义：如果数列{an}的任意连续三项均能构成一个三角形的三边长，则称{an}为“三角形”数列．对于“三角形”数列{an}，如果函数y=f（x）使得bn=f（an）仍为一个“三角形”数列，则称y=f（x）是数列{an}的“保三角形函数”，（n∈N*）．
（1）已知{an}是首项为2，公差为1的等差数列，若f（x）=kx，（k＞1）是数列{an}的“保三角形函数”，求k的取值范围；
（2）已知数列{cn}的首项为2010，Sn是数列{cn}的前n项和，且满足4Sn+1-3Sn=8040，证明{cn}是“三角形”数列；
（3）根据“保三角形函数”的定义，对函数h（x）=-x2+2x，x∈[1，A]，和数列1，1+d，1+2d（d＞0）提出一个正确的命题，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网