题目内容
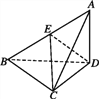
【题目】在四棱锥
中，
为正三角形，平面
平面
，
，
，
.
（1）求证：平面
平面
；
（2）求三棱锥
的体积；
（3）在棱
上是否存在点
，使得
平面?若存在，请确定点的位置并证明；若不存在，说明理由.
【答案】见解析
【解析】（1）因为
，
，所以
.
因为平面
平面
，平面
平面
，所以
平面
.（2分）
因为
平面
,所以平面
平面.（4分）
（2）如图，取
的中点
,连接
.
因为
为正三角形，所以
.
因为平面平面，平面平面，所以
平面，所以为三棱锥
的高.（6分）
因为为正三角形，
，所以
.
所以
.（8分）
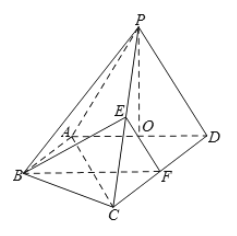
（3）在棱
上存在点
，当为的中点时，
平面.（9分）
如图，分别取
的中点
，连接
，所以
.
因为，
，所以
，所以四边形
为平行四边形，所以
.
因为
,所以平面
平面.（11分）
因为
平面
，所以
平面
.（12分）
练习册系列答案
相关题目
