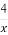Question

已知函数f(x)=2x-lo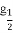x,实数a,b,c满足a<b<c,且满足f(a)f(b)f(c)<0,若实数x0是函数y=f(x)的一个零点,则下列结论一定成立的是(　　)

(A)x0>c (B)x0<c

(C)x0>a (D)x0<a

 

Answer 1

C

【解析】由于函数f(x)=2x-lo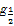x为增函数,故若a<b<c,f(a)f(b)f(c)<0,则有如下两种情况:①f(a)<f(b)<f(c)<0;②f(a)<0<f(b)<f(c),又x0是函数的一个零点,即f(x0)=0,故当f(a)<f(b)<f(c)<0=f(x0)时,由单调性可得x0>a,又当f(a)<0=f(x0)<f(b)<f(c)时,也有x0>a,故选C.